Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 133
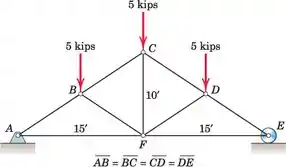
Determine a força em cada membro da carga treliça.
Passo 1
Neste caso, usamos simetria para dizer que AY = EY e eles têm 7,5 kips. Da afirmação de que a soma das forças é igual a zero e AX = 0, obtemos
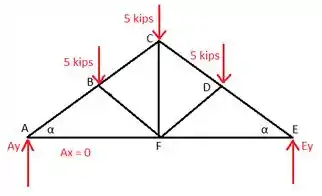
JUNTA A:
Passo 2
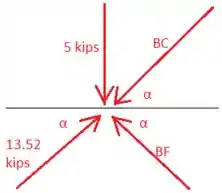
A junta B tem BC, BF e 13,52 kips agindo sobre si mesma,
JUNTA B:
Passo 3
O próximo ponto é a junta F, aqui CF, DF = BF, EF e 11,25 kips são parâmetros atuantes.
Usamos simetria EF = AF = 11,25 e DF = BF = 4,51
JUNTA F:
Resposta
Exercícios de Livros Relacionados
Uma suspensão de eixo duplo para uso em caminhões pequenos é mostrada na figura. A massa da estrutura central F é de 40 kg, e a massa de cada roda e elo conectado é de 35 kg com centro de massa de 680
Os projetistas de mecanismos de lâmpadas, como o mostrado na figura, geralmente contam com a fricção das juntas para ajudar a manter o equilíbrio estático. Para o presente problema, suponha que exista
Determine a força no cilindro hidráulico AB e a magnitude da reação do pino em O para a posição mostrada. A caçamba e sua carga têm um peso combinado de 4.000 libras com centro de gravidade em G. Você
O mecanismo de poda de uma serra de vara é mostrado enquanto corta um ramo S. Para a posição particular desenhada, o cabo de atuação é paralelo ao poste e carrega uma tensão de 30 lb. Determine a forç
A unidade de força A do trator-raspador tem uma massa de 4 Mg com centro de massa em G1. A unidade raspadora de reboque totalmente carregada B tem uma massa de 24 Mg com centro de massa em G2. O posic