Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 24
Um binário no sentido horário é aplicado ao cilindro circular, como mostrado. Determine o valor de necessário para iniciar o movimento para as condições , , , e . O atrito entre o cilindro e o bloco é insignificante.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar o valor mínimo do binário necessário para que o movimento inicie nas condições mostradas.
Então bora resolver! Vamos começar analisando o diagrama de corpo livre do bloco o qual o cilindro se apoia:
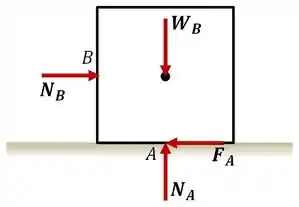
Onde o peso do bloco é:
Sabemos ainda que estamos na condição de atrito máximo, pois está na eminência de ocorrer o movimento, logo:
Passo 2
Pela condição de equilíbrio do corpo, podemos usar o somatório de forças nas direções e para determinar nossas incógnitas. Começando pelo eixo , temos:
Substituindo esse valor de na equação do Passo 1:
Fazendo o mesmo para o eixo :
Passo 3
Até aqui tudo certo né?! Agora vamos analisar o diagrama de corpo livre do cilindro separadamente.
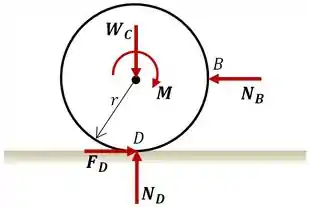
Onde o peso do bloco é:
Passo 4
Pela condição de equilíbrio do corpo, podemos usar o somatório de forças nas direções e para determinar nossas incógnitas. Começando pelo eixo , temos:
Com esse valor de , podemos calcular a força de atrito máxima entre a superfície e o cilindro:
Fazendo o mesmo para o eixo :
Ou seja, a força de atrito desenvolvida de fato entre o cilindro e a superfície é menor que a força de atrito máxima:
Logo, podemos concluir que o cilindro ainda não está deslizando.
Passo 5
Finalmente, fazendo o equilíbrio de momentos em torno do centro de gravidade do cilindro, podemos determinar o momento necessário para iniciar o movimento:
É só isso, galera!
Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 