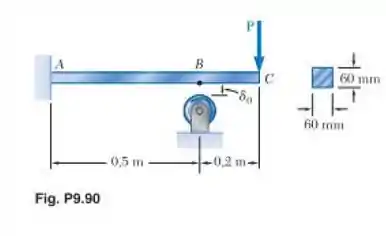
Antes de aplicar a carga P, havia uma folga de entre a viga em balanço AC e o suporte em B. Sabendo que E = 200 GPa, determine a intensidade de P para qual a deflexão em C é de 1 mm.

Tá legal! Vamos começar esse exercício encontrando o momento de inércia da nossa viga, como temos uma seção retangular, o momento de inércia será:

Vamos aproveitar e calcular o valor do termo EI, que também usaremos lá na frente. Então teremos:

Agora nós vamos considerar o diagrama para a nossa viga somente até o ponto B, para poder escrever a deflexão nesse ponto em função do dado, (lembre-se do momento gerado por P no ponto B), então teremos o seguinte DCL:

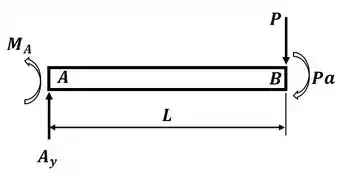
Agora podemos utilizar o apêndice D para pegar a deflexão máxima causada pelo carregamento, no nosso caso, temos o caso 1 e o caso 3, com carga e momento aplicados na ponta. E, para a situação inicial, onde tínhamos a folga , a deflexão máxima nesse caso será justamente esse valor, então podemos escrever:

Substituindo os valores conhecidos, chegamos na seguinte expressão:

Beleza, essa será nossa equação 1, vamos guardar ela.

Agora nós vamos considerar a viga como um todo, só que iremos dividir as forças P e a reação em B em dois carregamentos, então para o primeiro caso, teremos:

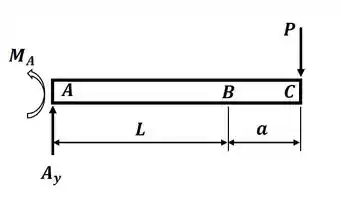
Nesse caso, a deflexão máxima será dada pelo caso 1 do apêndice D, onde teremos:

Agora, para o segundo carregamento, onde só teremos a força de apoio em B, nosso DCL será:

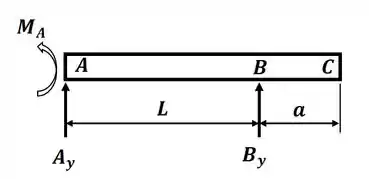
Agora, teremos que a inclinação e a deflexão no ponto B serão dadas pelas fórmulas do caso 1 do apêndice D, onde teremos:

E, agora, para encontrar a deflexão em C, basta somar a deflexão em B com a parcela rotacionada em B, onde teremos:

Agora temos que a deflexão total no ponto C será dada por:

Substituindo as expressões encontradas e o valor de dado no enunciado, teremos:

Essa é a nossa segunda equação para resolver nosso problema. Então, multiplicando a primeira equação por (-1,6) e somando com a segunda, teremos:

Shoow! Terminamos mais um, valeeu!