Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 82
Para o apoio de elastômero do Prblema 2.81 com e , determine o módulo de cisalhamento e a tensão de cisalhamento para a força lateral máxima e um deslocamento máximo
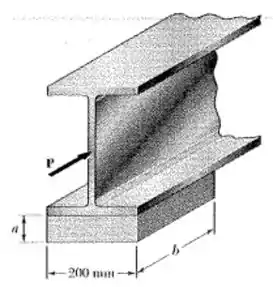
Passo 1
Para começar vamos anotar os dados que nós temos:
Para determinarmos a medida de , começamos aplicando a elação
Onde A é a área da base.
Passo 2
Para determinarmos a usaremos a relação
Onde é a tangente referente à variação do ângulo. Isso faz com que a força seja proporcional ao deslocamento relativo.
Devemos lembrar ainda que podemos representar também como
Isolando então o G teremos
Resposta
Exercícios de Livros Relacionados
Uma barra de 300 mm de comprimento e seção transversal retangular de 20 × 50m m consiste em duas lâminas de aço doce, cada uma com 6m m de espessura coladas a uma lâmina central de 8 mm de espessura,
Para a barra composta do Problema 2.106, de P cresce gradualmente desde zero até 375k N e depois retorna a zero, pede-se determinar a máxima deformação na barra, a máxima tensão em cada lâmica e, a de
Uma barra de 300 mm de comprimento e seção transversal retangular de 20 × 50m m consiste em duas lâminas de aço doce, cada uma com 6m m de espessura coladas a uma lâmina central de 8 mm de espessura,
A temperatura da barra composta do P r o b .2.43 é aumentada para 80 ° C . Sabendo-se que, para o aço E = 200G P aeα = 11,7.10 - 6° C - 1 , para o latão E = 105G P aeα = 20,9.10 - 6° C - 1 , e que nen
Uma barra de alumínio ( E = 70G P a ;α = 23,6.10 - 6° C - 1 ) e uma haste de aço ( E = 200G P a ;α = 11,7.10 - 6° C - 1 ) tem as dimensões mostradas, a uma temperatura de 20°C. A haste de aço é aqueci