Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 61

Uma barra de alumínio ( E = 70   G P a ;   α = 23,6   .   10 - 6   ° C - 1 ) e uma haste de aço ( E = 200   G P a ;   α = 11,7   .   10 - 6   ° C - 1 ) tem as dimensões mostradas, a uma temperatura de 20°C. A haste de aço é aquecida até que a barra de alumínio possa ser ajustada livremente nela. A temperatura de toda a montagem é então elevada para 150°C. Determinar a tensão final:

  1. Na barra;
  2. Na haste.

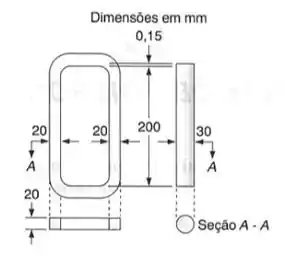
Passo 1

O enunciado nos dá as seguintes propriedades por cada material dados por:

  • Barra de alumínio

    • E = 70 G P a

    α = 23,6   .   10 - 6 1 ° C

  • Haste de Aço

    • E = 200 G P a

    α = 11,7   .   10 - 6 1 ° C

    A variação de temperatura vai ser dada por:

    ∆ T = 150 - 20 = 130 ° C

    L = 200   m m = 0,200   m

    Como precisamos determinar as deformações da barra de alumínio e as hastes de aço, vamos dividir em duas partes. Primeiro a deformação devido a temperatura e depois devido a carga que age nas estruturas, dessa maneira teremos que:

  • Barra de alumínio

    • A deformação devido a temperatura será:

    δ T A = L α A ∆ T

    δ T A = 200   .     23,6   .   10 - 6   .     130 = 0,6136   m m

  • Haste de aço

    • A deformação devido a temperatura será:

    δ T S = L α S ∆ T

    δ T S = 200   .     11,7   .   10 - 6   .     130 = 0,3042   m m

    Agora vamos analisar a deformação devido as cargas que agem na nossa barra, sabemos que a barra cabe dentro da haste, por isso sabemos que a barra irá empurrar a haste quando dilatar, e por reação a haste empurrará a barra, como podemos ver na figurinha abaixo.

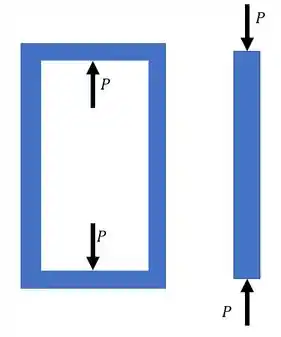
    Vamos então determinar as deformações devido as cargas agindo:

  • Barra de alumínio

    • Vamos começar a calcular a área da barra:

    A A = π D 2 4 = π 30 2 4 = 706,86   m m 2

    δ P A = P L E A = P   .   200 70   .   706,86   = 4,042   .   10 - 3 P

  • Haste de Aço

    • Vamos começar a calcular a área da barra:

    A S = 2   .     20 2 = 800   m m 2

    δ P S = P L E A = P   .   200 200   .   800   = 1,25 .   10 - 3 P

    Passo 2

    Agora precisamos garantir que a estrutura terá comprimentos iguais, com isso sabemos que, para a haste ela terá:

  • 200 mm do comprimento dela
  • Somado a temperatura que como é positiva irá fazer ela expandir
  • Somado a carga P que irá fazer ela se alargar também já que o sentido é de expansão

E para a barra teremos que:

  • 200 mm do seu comprimento
  • Somado a variação devido a temperatura
  • Somado aos 0,15 mm que ele tem amais que a haste
  • Subtraído a deformação devido a carga P, pois lembre que a temperatura expande e a força atua comprimindo, logo os sinais devem ser opostos.

E no fim das contas os dois (haste e barra) devem ser iguais, sendo assim teremos que:

200 + δ T S + δ P S = 200 + 0,15 + δ T A - δ P A  

Assim teremos que:

200 + 0,3042   + 1,25 .   10 - 3 P = 200 + 0,15 + 0,6136 - 4,042   .   10 - 3 P

Isolando teremos que:

1,25 .   10 - 3 P + 4,042   .   10 - 3 P = 200 + 0,15 + 0,6136 - 200 - 0,3042  

5,292 .   10 - 3 P = 0,4594

P = 86,81   k N

Passo 2

Se temos a carga e a área agora é só determinar as tensões:

σ B a r r a = - P A = 86,81 706,86 = - 0,1228   G P a = - 122,8   M P a

σ H a s t e = P A = 86,81 800 = 0,1085   G P a = 108,5   M P a

Resposta

  1. σ B a r r a = - 122,8   M P a
  2. σ H a s t e = 108,5   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 2.117 considerando que a temperatura da barra é incrementada até 150°C e depois reduzida até 25°C.
A barra AB tem uma área de seção transversal de 120 mm² e é feita de um aço elastoplástico com E = 200G P aeσ E = 250M P a . Sabendo que a força F aumenta de 0a250k N e depois diminui para zero, deter
Resolva o Problema 2.122, considerando que a = 180 m m .
Cada uma das quatros barras verticais que conectam os dois elementos horizontais rígidos é feita de alumínio ( E = 70G P a ) e tem seção transversal retangular e uniforme 10 x 40 mm. Para o carregamen
A barra de alumino ABC ( E = 69,6G P a ) , que consiste em duas partes cilíndricas AB e BC, deve ser substituída por uma barra de aço cilíndrica DE ( E = 200G P a ) do mesmo comprimento total. Determi