Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 48
Pelo apoio do Prob. 1.47, sabendo que o diâmetro do pino é d= 16 mm e que a magnitude da carga é P= 20 kN, determine (a) o fator de segurança do pino, (b) os valores exigidos de b e c se o fator de segurança para os elemento deve ser o mesmo a aquele encontrado na parte a para o
pino
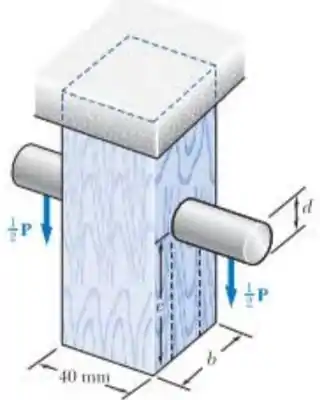
Passo 1
E ai gurizada tudo belezinha??? Primeiramente vamos calcular o fator de segurança do pino, mas antes vamos calcular a área.
Cisalhamento duplo
Calculando o fator de segurança:
Passo 2
Tensão na madeira:
Cisalhamento duplo: cada área é
Usando o “P” de menor valor:
Tem-se:
Resposta
- 2,92
Exercícios de Livros Relacionados
Para o eixo A B e a alavanca A C , mostrar que o efeito das tensões de cisalhamento, causadas pela carga transversal, devem ser incluídas para que se obtenha o valor exato da máxima tensão. L d1 3 1 +
Desprezando-se o efeito da concentração de tensões no escalonamento, determinar os menores diâmetros permissíveis para as barras maciças B C e C D . Usar τ a d m = 60M P a .
Sabendo-se que o diâmetro do tronco de cone mostrado é 38m m em A e 58m m em B , determinar a máxima tensão de cisalhamento: ( a ) em A ; ( b ) em B .
Sabendo-se que as barras B C e C D têm diâmetros de 24m m e 36m m , respectivamente, determinar a máxima tensão de cisalhamento em cada uma barra. Desprezar o efeito da concentração de tensões no esca
Sabendo-se que τ a d m = 50M P a , determinar o menor diâmetro permissível para o eixo maciço A B , quando P = 670N , l = 460m m e L = 75m m . Incluir o efeito das tensões de cisalhamento, causadas pe