Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 169
Sabendo-se que as barras e têm diâmetros de e , respectivamente, determinar a máxima tensão de cisalhamento em cada uma barra. Desprezar o efeito da concentração de tensões no escalonamento.
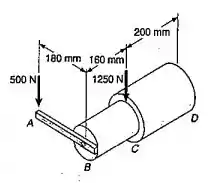
Passo 1
Fala aí galera, bora resolver mais uma questão de Resmat.
Esta questão nos pede para acharmos a máxima tensão de cisalhamento para as barras e Para isso, precisamos encontrar o momento fletor no eixo e a torção.
Primeiro, temos que encontrar a torção:
Para
Passo 2
Em seguida, vamos calcular os momento em relação ao ponto :
Com isso, podemos encontrar o momento fletor nos pontos críticos, dado por:
Passo 3
E então, vamos aplicar a relação entre torque e tensão cisalhante:
Por fim, vamos repetir o processo para a outra barra, e assim, temos:
Resposta
Exercícios de Livros Relacionados
Determinar os planos principais e as tensões principais para o estado plano de tensões, resultante da superposição dos dois estados planos de tensões mostrado, considerando as tensões do 2º plano por
Uma força de 19,5 kN é aplicada no ponto D da barra de ferro fundido mostrada. Sabendo-se que a barra tem um diâmetro de 60 mm, determinar as tensões principais e a máxima então de cisalhamento nos po
Várias forças são aplicadas à montagem tubular indicada. Sabendo-se que os diâmetros, interno e externo, do tubo são iguais a 38 mm e 45 mm, respectivamente, determinar os planos e as tensões principa
Duas forças são aplicadas como mostrado na barra AB, que é soldada ao cilindro DE, de diâmetro 50mm. Considerando que todas as tensões permanecem abaixo do limite de proporcionalidade, determinar as t
Uma força vertical de 4kN é aplicada no ponto A de um componente de maquina mostrado. Determinar as tensões principais e a máxima tensão de cisalhamento no:Ponto HPonto K