Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 170
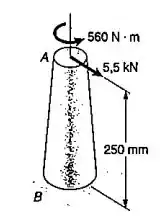
Sabendo-se que o diâmetro do tronco de cone mostrado é em e em , determinar a máxima tensão de cisalhamento: em ; em .
Passo 1
Fala aí galera, bora pra mais uma questão de Resmat.
Este problema nos pede para determinarmos a máxima tensão de cisalhamento em duas seções, e . Primeiro, sabemos que a máxima tensão de cisalhamento em uma seção circular é dada por:
Com isso, vamos calcular o momento de inércia, dado por:
Para a seção , temos:
Já para , temos:
Passo 2
Por fim, basta substituirmos na fórmula da máxima tensão de cisalhamento em uma seção circular. Para , temos:
Vamos repetir o processo para . Fica assim:
Resposta
Exercícios de Livros Relacionados
No eixo de um automóvel atuam as forças e o torque mostrado. Sabendo-se que o diâmetro do eixo é de 30 mm, determinar os planos principais e as tensões principais no ponto H, localizado no cume da sup
Sabendo-se que o tubo estrutural mostrado tem uma espessura uniforme de parede de 6,35 mm, determinar, para o carregamento dado, a máxima tensão de cisalhamento e a correspondente orientação dos plano
Sabendo-se que o tubo estrutural mostrado tem uma espessura uniforme de parede de 6,35 mm, determinar, para o carregamento dado, a máxima tensão de cisalhamento e a correspondente orientação dos plano
Três forças são aplicadas, como mostrado, a uma viga em balanço. Determinar as máximas tensões de cisalhamento e as orientações nos pontos H e K.
Determinar os planos principais e as tensões principais para o estado plano de tensões, resultante da superposição dos dois estados planos de tensões mostrado, considerando as tensões do 2º plano por