Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 7
Um apoio em T sustenta as quatro cargas mostradas na figura. Determine as reações em A e B (a) se a = 250 mm, (b) se a = 175 mm.
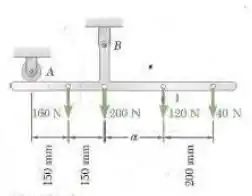
Figura P4.7
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Precisamos determinar as reações em A e B para os casos em que a= 250 mm (letra a) e que a= 175 mm (letra b)
Olhando para a imagem do enunciado, podemos notar que que todas as forças estão em (Newtons) e todas as medidas estão em mm (milímetros). Portanto, não será necessário converter unidades.
Podemos ver também que ambos os apoios provocam reações apenas na vertical.
Passo 2
Podemos considerar o seguinte diagrama de corpo livre:
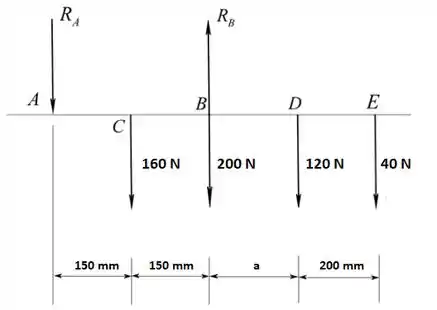
Analisando o diagrama podemos aplicar o somatório dos momentos em torno de A para determinar a reação em A ():
=0
Passo 3
Uma vez determinado poderemos aplicar o somatório das forças na vertical para determinar :
Passo 4
Aplicaremos o valor de a igual a 250 mm (letra a) nas relações encontradas nos passos 2 e 3:
indica a reação no ponto B e o resultado positivo mostra que o sentido é o mesmo representado no diagrama de corpo livre, ou seja, para cima.
Agora utilizaremos esse valor na relação encontrada no passo 3 para encontra :
indica a reação no ponto A e o resultado positivo mostra que o sentido é o mesmo representado no diagrama de corpo livre, ou seja, para baixo.
Passo 5
Aplicaremos o valor de a igual a 175 mm (letra b) nas relações encontradas nos passos 2 e 3:
indica a reação no ponto B e o resultado positivo mostra que o sentido é o mesmo representado no diagrama de corpo livre, ou seja, para cima.
Agora utilizaremos esse valor na relação encontrada no passo 3 para encontra :
indica a reação no ponto A e o resultado positivo mostra que o sentido é o mesmo representado no diagrama de corpo livre, ou seja, para baixo.
Resposta
Letra a):
Letra b):