Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 5

Dois caixotes, de massa 350 kg cada, são colocados na caçamba de uma caminhonete de 1.400 kg. Determine as reações em cda uma ds duas (a) rodas traseiras A, (b) rodas dianteiras B.

Figura P4.5

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.2FA

Precisamos determinar a reação em cada uma das rodas da caminhote. Chamaremos a reação em cada uma das rodas traseiras de e a das rodas dianteiras de .

É apresentada a massa dos dois caixotes () e da caminhote (). Devemos calcular o peso dos caixotes e da caminhote, multiplicando suas massas pela aceleração da gravidade (). Dessa forma:

Agora temos todas as forças peso em N (Newtons) e todas as medidas estão em m (metros). Portanto, não será necessário converter unidades.

Passo 2

Agora podemos considerar o seguinte diagrama de corpo livre:

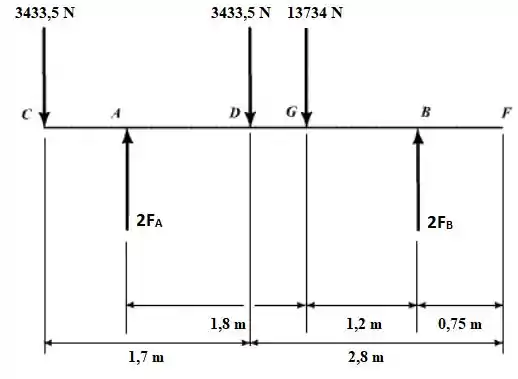
As forças nas posições A e B foram representadas com e pois em cada uma dessas posições horizontais temos duas rodas.

Analisando o diagrama podemos aplicar o somatório dos momentos em torno de B para determinar as reações em cada uma das rodas traseiras ():

indica a resultante em cada uma das rodas traseiras e o resultado positivo mostra que o sentido é o mesmo representado no diagrama de corpo livre, ou seja, para cima.

Passo 3

Uma vez determinadas as forças , faremos o somatório de forças verticais para determinar a força em cada uma das rodas dianteiras (). Temos que:

indica a resultante em cada uma das rodas dianteiras e o resultado positivo mostra que o sentido é o mesmo representado no diagrama de corpo livre, ou seja, para cima.