Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 80
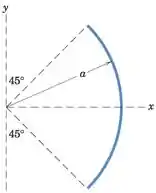
O arco circular é girado 360 em torno do eixo y. Determine a área da superfície externa S do corpo resultante, que é uma parte de uma casca esférica.
Passo 1
Lembre-se dos teoremas de Pappus que a superfície externa de um corpo pode ser encontrada pela fórmula:
E o Volume pode ser encontrado pela fórmula:
representa a distância do centro de massa do eixo de revolução
Este problema é exatamente o Problema Amostra 5/10, então não tenho certeza de por que o autor considerou isso um problema não resolvido, mas tentarei explicar o problema com mais detalhes. Precisamos encontrar a distância do centro de massa do eixo y. Olhando para o problema de amostra 5/1:
Passo 2
Em nosso caso e , então:
Em seguida, precisamos encontrar , uma vez que a revolução é 360, escrevemos:
Em seguida, estamos procurando encontrar a Área externa aqui, então usaremos a primeira fórmula do Teorema de Pappus:
Passo 3
A última coisa de que precisamos é o Comprimento, neste caso é o perímetro. Como queremos encontrar o perímetro de um comprimento de arco circular que se estende por 90 (quarto de círculo), escrevemos:
Temos tudo o que precisamos para encontrar a área para: