Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 40
A barra fina e uniforme de comprimento l é colocada na abertura de largura d no ângulo 30∘ mostrado. Para qual intervalo de l/d a barra permanecerá em equilíbrio estático? O coeficiente de atrito estático em A e B é
Passo 1
O enunciado pede que a gente determine qual intervalo de l/d a barra permanecerá em equilíbrio estático
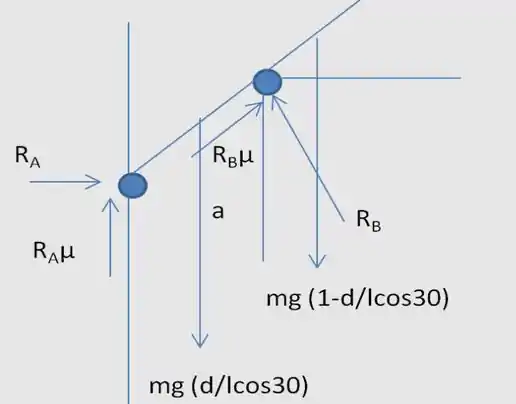
Tomando a condição de escorregamento onde a haste escorrega na direção para baixo e aplicando o equilíbrio, obtém-se duas equações em duas incógnitas RA, RB
Equação 1
Equação 2
Multiplicando EQ(1) por
Substituindo Eq(2) por eq (1)
Com
por substituição
Passo 2
Para um momento de equilíbrio sobre B
Agora considere a condição de escorregamento onde a haste vira para cima e escorrega na direção para cima. A aplicação de equilíbrio dá duas equações em duas incógnitas RA, RB
Equação 1
Equação 2
Multiplicando eq(1) por
Adicionando Eq(1) e (2)
Passo 3
Para um momento de equilíbrio sobre B obtemos
Procedendo derivamos a equação
Então, sua taxa é
O limite superior é próximo, mas não exatamente igual à resposta dada no livro; 8,14.