Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 37

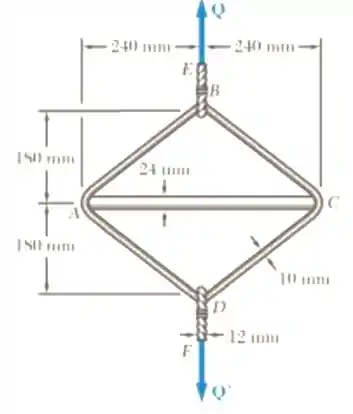
Um aro em forma de losango de aço ABCD com comprimento de 1,2 m e com 10 mm de diâmetro é colocado para envolver uma barra de alumínio AC com 24 mm de diâmetro conforme mostra a figura . São utilizados os cabos BE e DF, cada um com 12 mm de diâmetro para aplicar a carga Q. Sabendo que a resistência do aço utilizado para o aro e os cabos é de 480 MPa e que o limite de resistência do alumínio utilizado na barra é 260 MPa determine a máxima carga Q que pode ser aplicada quando se adota um coeficiente de segurança 3 para todos os elementos.

Passo 1

E ai gurizada tudo belezinha??? Primeiramente vamos analisar o diagrama de corpo livre :D

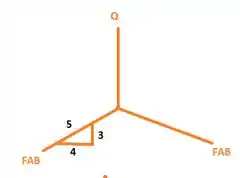
Usando a articulação B como um corpo livre e considerando a simetria

(1)

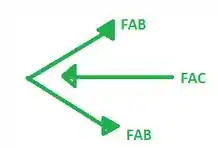
Usando a articulação A como um corpo livre e considerando a simetria

(2)

Substituindo 1 em 2 temos:

(2)

Com base na força do cabo BE

Passo 2

Com base na força da haste AC

A carga máxima real QU a menor é 9,27 75 kips que foi obtida no passo 1

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o método da sec 7.4 resolver o problema 7.6

Usando o método da sec 7.4 resolver o problema 7.4

Usando o método da sec 7.4 resolver o problema 7.5

A viga AB suporta duas cargas concentradas P e Q. A tensão normal devido a flexão na borda inferior da seção transversal da viga é de + 55MPa em D e 37,5 MPa em F. Pede-se a) desenhar os diagramas de

As vigas AB, BC e BD tem seções transversais como mostrado e são articuladas por pinos conectores em B e C. Sabendo se que σadm= 150 MPa na tração σadm= -120 MPa na compressão a) o maior valor admissí