Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 44
Para a conexeão e carregamento de Prob. 1,43, determine o coeficiente de segurança, sabendo que o comprimento de cada junta é L=180 m
180 m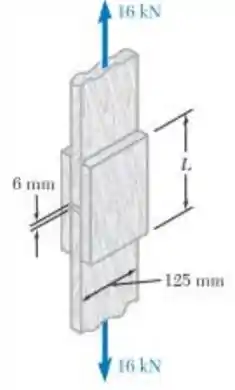 
Passo 1
E ai gurizada tudo belezinha??? Primeiramente vamos relembrar a equação para encontrarmos a área:
Como existem 2 superfícies de contato, temos:
Calculando o fator de segurança temos:
Resposta
Exercícios de Livros Relacionados
Uma viga em balanço A B é de altura h constante e de largura b variável. Sabendo-se que a viga deve ser de resistência constante, expressar b em termos de b 0 ,x e L , se o único carregamento é: (a) u
Uma viga em balanço A B é de altura h constante e de largura b variável. Sabendo-se que a viga deve ser de resistência constante, expressar b em termos de b 0 ,x e L , se o único carregamento é: (a) u
Duas placas de cobertura, cada uma com 16m m de espessura, são soldadas a uma viga de perfil laminado W690 × 125 , como mostrado. Sabendo-se que l = 4,4 m e b = 30 0m m , determinar a máxima tensão no
Uma viga A B é um sólido de revolução de diâmetro variável d . Para a porção A C da viga, expressar d , em termos de d 0 ,x e L , sabendo-se que a viga deve ser de igual resistência quando suporta o c
Duas placas de cobertura, cada uma com 12,7m m de espessura, são soldadas a uma viga de perfil W 530 × 92 , como mostrado. Sabendo-se que l = 4,2 m e b = 250m m , determinar a máxima tensão normal em