Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas - Ex. 54
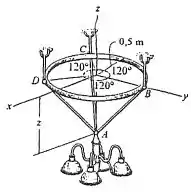
O aro pode ser ajustado verticalmente entre três cabos de mesmo comprimento a partir dos quais o lustre de 100 kg é suspenso. Se o aro permanece no plano horizontal e , determine a tração em cada cabo.
Passo 1
Para encontrar o valor da força em cada cabo, o que deve ser feito primeiramente é o diagrama de corpo livre no qual serão representadas as forças envolvidas.
Como o aro possui uma simetria (divide-se em partes com o mesmo comprimento e mesmo ângulo) e as distâncias do seu centro até os pontos B, C e D são iguais, então a tração será a mesma em cada cabo.
Podemos adotar que o ângulo entre o eixo z e cada cabo é e é dado por:
Tem-se que o lustre exerce uma força peso para baixo que tem intensidade de .
Passo 2
Logo, fazendo o diagrama de corpo livre tem-se:
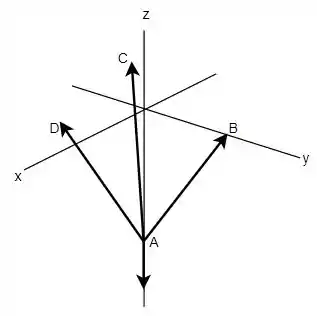
E, então, observando o desenho feito consegue-se montar as equações de equilíbrio.
Passo 3
O equilíbrio requer quer que o somatório de forças em cada dimensão seja nulo. Porém, a única força dada pelo enunciado está no eixo z. Logo, adotando o sentido dos eixos mostrado no desenho do enunciado: