Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 100
O suporte de luz é articulado livremente em e é restringido pelo pino fixo na fenda lisa em . Calcule a magnitude da força suportada pelo pino em sob a ação do binário aplicado de .
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a magnitude da reação suportada pelo pino devido ao binário de aplicado no ponto . Vamos fazer o diagrama de corpo livre do sistema para ficar mais fácil de entender.
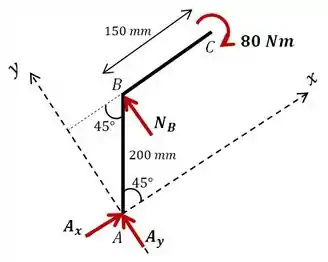
Show de bola! Começamos então pelo equilíbrio de momento em torno de , dessa forma eliminados duas das incógnitas e conseguimos determinar a reação :
Passo 2
Feito isso, podemos fazer o equilíbrio de forças nos eixos e para encontrar e . Começando pelo somatório de forças na direção :
E para a direção :
Agora fica fácil calcular a resultante em né?
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 