Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 8
O automóvel tem massa de e centro de massa em . Determine a força de reboque exigida para mover o carro. Os freios dianteiros e traseiros estão acionados. Considere .
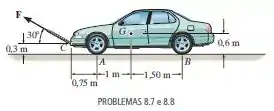
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Aqui queremos o valor de para que o carro se mova. Vamos analisar o equilíbrio de momentos com relação ao ponto :
Substituindo os valores conhecidos, temos que:
Passo 2
Analisando o equilíbrio horizontal, temos que:
Onde e representam as forças de atrito nos pontos e respectivamente. Portanto:
Substituindo a equação que encontramos no passo anterior, temos que:
Analisando o equilíbrio vertical, temos que:
Substituindo os valores conhecidos, temos que:
Resposta
Exercícios de Livros Relacionados
Uma força P = m g / 6 é necessária para abaixar o cilindro a uma velocidade constante lenta com a corda fazendo 1 1 4 voltas em torno do eixo fixo. Calcule o coeficiente de fricção μ entre o cabo e o
Determine a faixa de pesos W do uniforme barra delgada para a qual o sistema estará em equilíbrio. Despreze o atrito em todos os rolamentos.
Grampos de placa para serviço pesado com cames de cunha são projetados para ser usado em pares para levantar e transportar grandes placas de aço. À medida que cada came começa a fazer efeito, a placa
Um carrinho de mão carregado é colocado em uma inclinação acidentada. O peso combinado do carrinho de mão e sua carga atua no centro de gravidade G. (a) Determine o ângulo máximo θ para o qual o carri
O corpo homogêneo com dois pés pequenos e duas rodas ideais estão em repouso na inclinação acidentada. (a) Suponha sem derrapagem e determine o valor máximo do ângulo θ para o qual o corpo não vira em