Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 33
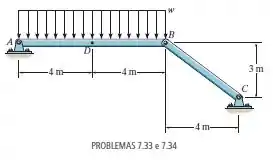
Determine as forças normal e cortante e o momento fletor em uma seção que passa pelo ponto . Considere .
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Queremos as forças normal e cortante e o momento fletor nos pontos .
Aqui, podemos considerar a nossa viga como dois elementos separados, para fins de análise. Isto pode ser feito por causa do pino em que separa as barras e .
Vamos construir o diagrama de corpo livre de
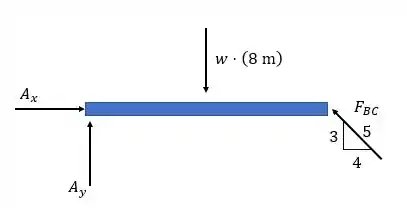
Considerando o momento em , temos que:
Sabendo que , temos que:
Analisando o equilíbrio horizontal, temos que:
Analisando o equilíbrio vertical, temos que:
Ou:
Passo 2
Se cortarmos a seção , podemos descobrir os valores das reações internas no ponto :
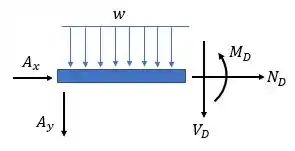
Vamos analisar o equilíbrio com relação à direção da normal:
Ou:
Agora analisando o equilíbrio com relação a cortante, temos que:
Substituindo os valores, temos que:
Ou:
Analisando o equilíbrio com relação ao momento fletor, temos que:
Ou: