Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 46

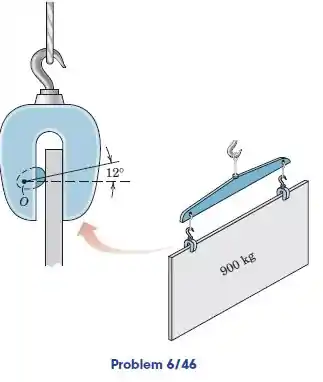
Grampos de placa para serviço pesado com cames de cunha são projetados para ser usado em pares para levantar e transportar grandes placas de aço. À medida que cada came começa a fazer efeito, a placa desliza ligeiramente contra a superfície vertical da braçadeira e, portanto, gera limitação atrito estático nessa interface. Se o coeficiente de atrito estático para todas as superfícies de contato é de 0,30, calcular a força R suportada pelo pino em O para cada uma das duas braçadeiras simetricamente colocadas no Placa de 900 kg.

Passo 1

Oi pessoal? Vamos para mais um exercício?

Consideremos o deslocamento virtual S causado devido à força da mola:

S = θ - π 2

A energia armazenada na mola é dada pela seguinte equação:

W s = 1 2 k S 2

Substituindo os dados, temos que:

W s = 1 2 k ⋅ θ - π 2 2

O deslocamento virtual devido ao peso do bloco é dado por:

X = L 2 + L sen ⁡ θ

O trabalho realizado devido ao peso do bloco é dado por:

W b = W ⋅ X

Portanto:

W b = W L 2 + L sen ⁡ θ

A energia total do sistema será:

V = W s + W b

V = 1 2 k ⋅ θ - π 2 2 + W L 2 + L sen ⁡ θ

Passo 2

A condição de equilíbrio do sistema é a seguinte:

d V d θ = 0

Portanto:

d d θ 1 2 k ⋅ θ - π 2 2 + W L 2 + L sen ⁡ θ = 0

1 2 k ⋅ 2 θ - π 2 + W 0 + L cos ⁡ θ = 0

- W L cos ⁡ θ = k θ - π 2

Podemos fazer uma aproximação para a serie do cosseno que vale:

cos ⁡ θ = 1 - θ 2 2

Portanto:

W = k L 1 - θ 2 2 θ - π 2

Resposta

W = k L 1 - θ 2 2 θ - π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força P máxima que pode ser aplicada sem causar o movimento da caixa de 100 kg com centro de gravidade em G . O coeficiente de atrito estático no piso é μ s = 0 , 4 .
Determine a força P máxima que pode ser aplicada sem causar o movimento das duas caixas de 50 kg. O coeficiente de atrito estático entre cada caixa e o piso é μ s = 0,25 .
A haste uniforme com centro de massa em G é suportada pelas estacas A e B, que são fixadas na roda. Se o coeficiente de atrito entre a haste e os pinos for μ, determine o ângulo θ através do qual a ro
O semicilindro sólido de massa me raio r é rolado através de um ângulo θ pela força horizontal P. Se o coeficiente de atrito estático é μs, determine o ângulo θ no qual o cilindro começa a deslizar na
O carro de 1.600 kg está apenas começando a negociar a rampa de 16 ∘. Se o carro tiver tração traseira, determine o coeficiente mínimo de atrito estático exigido em B.