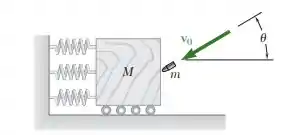
Uma bala de massa é atirada com velocidade formando um ângulo com a horizontal e se aloja em um bloco de madeira de massa . O bloco pode rolar sem atrito no piso duro e é impedido por molas de atingir a parede. Determine as componentes horizontal e vertical do impulso da força exercida pelo bloco na bala.

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão. Para o sistema bloco e bala , o momento na direção horizontal é conservado, portanto:

Sabemos que a bala vai alojar no bloco. Por isso, a velocidade da bala e do bloco serão iguais. Portanto:

Agora, para encontramos as componentes horizontal e vertical do impulso, podemos utilizar a seguinte relação:

Que nos diz que a quantidade de movimento linear de uma partícula no instante pode ser obtida adicionando-se à sua quantidade de movimento no instante e os impulsos das forças exercidas sobre a partícula durante o intervalo de tempo de a .

Primeiro, vou esboçar um esquema para que você visualize melhor o problema:

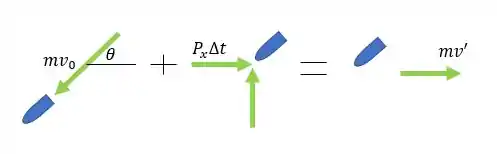
Com as componentes decompostas, temos que o impulso no eixo horizontal é dado por:

E para a componente vertical, temos:

É isso, galera. Bora zerar esse livro!