Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 153
A fim de testar a resistência ao impacto de uma corrente, ela é suspensa por uma viga rígida de apoiada em duas colunas. Uma barra presa no último elo é, então, golpeada por um bloco de que cai a uma altura de . Determine o impulso inicial exercido sobre a corrente e a energia absorvida pela corrente, considerando que o bloco não dá rebote na barra e que as colunas de apoio da viga são perfeitamente rígidas e equivalentes a duas molas perfeitamente elásticas.
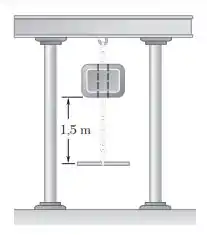
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão. Primeiro, vamos encontrar a velocidade do bloco antes do impacto , para isso, vamos utilizar a conservação de energia mecânica:
Onde é a energia potengial gravitacional, portanto:
No instante após o impacto o bloco tem , logo:
Assim, substituindo na equação de conservação de energia mecânica, e lembrando que no instante inicial não há velocidade e, portanto, , temos que:
Passo 2
Com isso, vamos calcular o impulso para o caso em que temos colunas rígidas. Para isso, podemos utilizar a seguinte relação:
Que nos diz que a quantidade de movimento linear de uma partícula no instante pode ser obtida adicionando-se à sua quantidade de movimento no instante e os impulsos das forças exercidas sobre a partícula durante o intervalo de tempo de a .
Primeiro, vou esboçar um esquema para que você visualize melhor o problema:
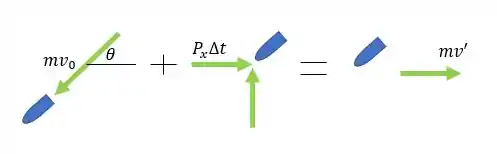
Com as componentes decompostas, temos que o impulso no eixo horizontal é dado por:
E para determinarmos a energia, temos que saber que toda a energia cinética vai ser absorvida pelas colunas, portanto:
É isso, galera. Bora zerar esse livro!