Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 175

Uma barra de 18   m m de diâmetro deve ser encurvada devido às cargas aplicadas, como mostrado. Sabendo-se que P = 200   N e Q = 0 , determinar a máxima tensão de cisalhamento e a máxima tensão normal, na extremidade A . Desprezar o efeito das tensões de cisalhamento, causadas por cargas transversais.

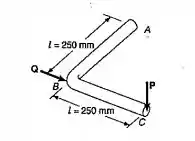
Passo 1

Fala aí galera, bora pra mais uma questão de Resmat.

O primeiro passo é determinar o momento torsor, temos:

T = Q × l T = 0

Em seguida, vamos encontrar a máxima tensão de cisalhamento, que é dada por:

τ m á x = T c J

Onde c é o raio da barra e J o momento polar de inércia da área da seção transversal. Substituindo, temos:

τ m á x = 0 c π 2 c 4 τ m á x = 0

Passo 2

Em seguida, vamos encontrar a máxima tensão normal. Para isso, vamos encontrar o momento na barra B C , temos:

M = P × l M = 200 × 0 , 250 M = 50   N

Com isso, vamos substituir na fórmula da tensão máxima e encontrarmos o que foi pedido. Fica assim:

σ m á x = M c J σ m á x = 50 π 2 0,009 3 σ m á x = 43,66   M P a

Resposta

τ m á x = 0

σ m á x = 43,66   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as equações das curvas dos diagramas da força cortante e do momento fletor, para a viga com carregamento indicado. (Adotar a origem no ponto A.)
Determine as equações das curvas dos diagramas da força cortante e do momento fletor, para a viga com carregamento indicado. (Adotar a origem no ponto A.)
Determine as equações das curvas dos diagramas da força cortante e do momento fletor, para a viga com carregamento indicado. (Adotar a origem no ponto A.)
Para o estado de tensões dado, determinar: (a) a orientação dos planos de máxima tensão de cisalhamento, no plano; (b) a tensão cisalhante máxima; (c) a correspondente tensão normal.
Para o estado de tensões dado, determinar: (a) a orientação dos planos de máxima tensão de cisalhamento, no plano; (b) a tensão cisalhante máxima (c) a correspondente tensão normal.