Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 12

Para o estado de tensões dado, determinar: (a) a orientação dos planos de máxima tensão de cisalhamento, no plano; (b) a tensão cisalhante máxima (c) a correspondente tensão normal.

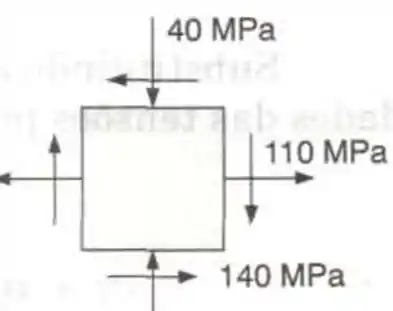
Passo 1

Para resolver essa questão a primeira coias e a mais importante é saber identificar corretamente as tensões normais e cisalhantes, neste caso será o seguinte:

σ x = 110   M P a

σ y = - 40   M P a

τ x y = - 140   M P a

Passo 2

O segundo passo, que já consiste na resolução da letra a , é a determinação dos planos de máxima tensão de cisalhamento, no plano:

t g 2 θ = - σ x - σ y 2 ⋅ τ x y

Substituindo:

t g 2 θ = - 110 - ( - 40 ) 2 ⋅ 140

t g 2 θ = - 0,5357

2 θ = a r c t g - 0,5357 = - 28,18 °

θ = - 28,18 ° 2

θ = - 14,9 °

Além disso precisamos somar 90° à esse ângulo, porque 90° corresponde à metade do suplemento (180°) do ciclo de Mohr.

θ = - 14,9 ° ; 75,1 °

Passo 3

A provável letra B do enunciado pede a tensão cisalhante máxima que é dada por:

τ m á x = σ x - σ y 2 2 + τ x y 2

Substituindo:

τ m á x = 110 - - 40 2 2 + 140 ²

τ m á x = 25225

τ m á x = 158,82   M P a

Passo 4

A letra C pede a correspondente tensão normal que é só fazer a média entre σ x e σ y :

σ = σ x + σ y 2

σ = 110 - ( - 40 ) 2 = 75   M P a

Resposta

a)

θ = - 14,9 ° ; 75,1 °

b)

τ m á x = 158,82   M P a

c)

σ = 75   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar o máximo
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar o máximo
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar o máximo
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar o momento
Assumindo que a reação do solo sobre a viga, de baixo para cima, se distribui uniformemente, desenhar os diagramas de força cortante e de momento fletor para a viga com carregamento mostrado e determi