Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 106

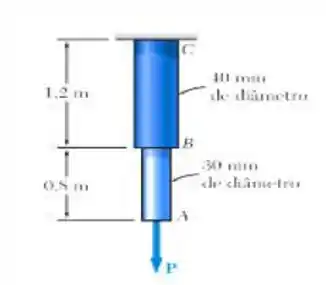
A barra ABC consiste em duas parte cilíndricas AB e BC: ela é feita de um aço doce considerado elastoplástico com E = 200   G P a   e   σ E = 250   M P a . Uma força P é aplicada à barra até que sua extremidade A tenha se movido para baixo por δ m = 5   m m . Determine o valor máximo da força P e a deformação permanente da barra depois que a força for removida.

Passo 1

Fala aí gurizada tudo belezinha?? O exercício pede para que a gente determine o valor máximo da força P e a deformação permanente da barra depois que a força for removida, então vem comigo :D

Primeiramente vamos determinar a área das seções AB e BC respectivamente e vem comigo :D

A A B = π 4   x   30 2 = 706,86   m m 2 = 706,86   x   10 - 6 m 2 A B C = π 4   x   40 2 = 1,25664   x   10 3   m m 2 = 1,25644     x   10 - 3 m 2

Agora podemos determinar a carga P , vejam que barbadinha

P m a x = A m i n σ Y

P = 706,86   x   10 - 6   x   250   x   10 6 = 176,715   x   10 3 N

Passo 2

E o alongamento é dado pela relação da carga P , módulo de elasticidade e área, venham comigo !!!

δ ' = P ' L A B E A A B + P ' L B C E A B C = 176,715   x   10 3   x   0,8 200   x   10 9   x   706,86   x   10 - 6 + 176,715   x   10 3   x   1,2 200   x   10 9   x     1,25664     x   10 - 3

δ ' = 1,84375   x   10 - 3 , = 1,84375   m m  

δ P = δ m = δ ' = 5 - 1,84375 = 3,17   m m

Resposta

P m a x = 176,7   k N δ P = 3,16   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o P r o b .1.49 , assumindo que a estrutura deve ser reprojetada para utilizar pinos de 8m m de diâmetro em A e C, assim como também em B, e que nenhuma outra modificação deve ser feita.
Na estrutura de aço mostrado, um pino de 6 m m de diâmetro é usado em C , enquanto que em B e D usam-se pinos de 10m m de diâmetro. A tensão de cisalhamento última para todas as ligações é de 150M P a
Resolver o P r o b .150 , assumindo que a estrutura deve ser reprojetada para utilizar pinos de 11,5m m de diâmetro em B e D, e que nenhuma outra modificação deve ser feita.
Resolver o P r o b .1.50 , assumindo que a estrutura deve ser reprojetada para utilizar pinos de 12 m m de diâmetro em B e D , e que nenhuma outra modificação deve ser feita.
Um fio de Nylon está sujeito a uma tração de 9,0 N . Sabendo-se que E = 3,45G P a e que a máxima tensão normal admissível é de 40M P a , determinar:O diâmetro necessário para o fio;O correspondente ac