Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 96
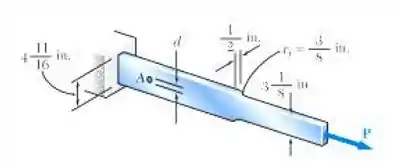
(a) para , determine a tensão máxima na placa mostrada, (b) resolva a parte a, supondo que não seja feito o furo em A.
Passo 1
Fala aí gurizada tudo belezinha ??? O enunciado pede que a gente determine a tensão máxima considerando e não considerando a presença do orifício, então , venham comigo !!!
Considerando a relação do raio diâmetro do elemento temos:
A área é obtida através da seguinte maneira:
Então temos a seguinte tensão:
Passo 2
Sem considerar o orifício podemos considerar a relação do raio diâmetro do elemento temos
A área é obtida através da seguinte maneira:
Então temos a seguinte tensão:
Resposta
- Com furo e filetes: 17,47 ksi
- Sem buraco: 17,47 ksi
Exercícios de Livros Relacionados
Duas cargas verticais são aplicadas ao pino B da montagem indicada. Sabendo-se que o diâmentro do pino usado em cada ligação é de 15,2m m , determine o valor máximo da tensão normalmédia na (a) haste
Determine a menor área admissível para a seção transversal da barra D E da treliça mostrada, se para o carregamento dado, a tensão normal nesta barra não deve ultrapassar 138M P a .
Para a treliça e carregamento mostrado, determine a tensão normal na barra B D . Sabendo-se que a área da seção transversal da barra é de 1 . 290m m ² ².
Determine a menor área admissível para a seção transversal da barra D E da treliça mostrada se para o carregamento dado, a tensão normal nesta barra não deve ultrapassar 200M P a .
Para a treliça e carregamento mostrado, determine a tensão normal na barra A D . Sabe-se que a área da seção transversal da barra é de 1.200m m ² ².