A barra ACB é engastada aos suportes rígidos e está ausente de tensões a uma temperatura de . O aço é assumido elastoplástico com e . A temperatura de ambas as porções da barra é então elevada para . Sabendo-se que :

1. A tensão em ambas as porções da barra;
2. O deslocamento do ponto C.

O enunciado nós da os seguintes dados sobre o nosso problema

Agora precisamos fazer duas coisas para resolver o nosso problema, que é definir a tensão residual do nosso problema, que é usar a equação de equilíbrio e usar a fórmula de compatibilidade, sendo assim teremos que:

• Equação de equilíbrio

A equação de equilíbrio é dada por:



Assim a fórmula será dada por:

Mas não conseguimos determinar os valores por essa fórmula, por isso temos que usar a nossa equação de compatibilidade, então o nosso primeiro passo é supor que o nosso problema seja elástico, e sabendo dessa informação, calculamos as tensões, e a que ultrapassar o valor usaremos como base para calcular a tensão residual, com isso vamos ter o seguinte:

• Equação de compatibilidade

Sabemos que o somatório de deformações totais nesse trecho tem que ser zero. Com isso teremos que:

E sabemos que:

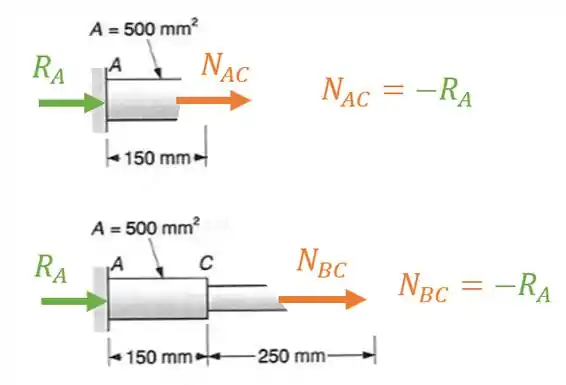
Substituindo teremos que:

A tensão em ambas as barras seriam:

Como a tensão no trecho BC é superior a tensão admissível, a tensão real que deve agir nele é a tensão admissível, sendo assim teremos que:

Agora pensa comigo, como a força no trecho AB e BC devem ser iguais, precisamos recalcular a tensão no trecho AC, sendo assim precisamos redefinir a força, com isso teremos que:

Negativo pois temos que lembrar que se trata de uma tensão de compressão, ou seja, negativa.