Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 68

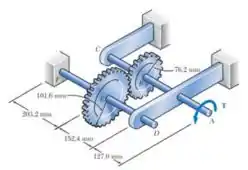
Dois eixos de aço, ambos com diâmetro de 19,1 mm, estão conectados às engrenagens mostradas na figura. Sabendo que G = 77,2 GPa e que o eixo DF está fixo em F, determine o ângulo de rotação da extremidade A quando lhe é aplicado um torque de 84,7   N ∙ m em A. (Ignore a energia de deformação em virtude da flexão dos eixos.)

Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso

cálculo:

Equação trabalho-energia:

1 2   T A φ A = U

φ A = 2 U T A

Porção AB do eixo ABC:

T A B = T A = 750   l b ∙ i n .

L A B = 5 + 6 = 11   i n .

J A B = π 2   d 2 4 = π 2 0,75 2 4 = 31,063 × 1 0 - 3 i n 4  

U A B = T A B 2 L A B 2 G J A B = 750 2 11 ( 2 ) ( 11,2 × 10 6 ) ( 31,063 × 10 - 3 ) = 8,892   i n . ∙ l b

Passo 2

Porção BC do eixo ABC:

U B C = 0

Engrenagem B:

F B E = T B r B = T A B r B = 750 3 = 250   l b

Engrenagem E:

T E = r E F B E = 4 250 = 1000   l b ∙ i n .

Porção DE do eixo DEF:

U D E = 0

Passo 3

Porção EF do eixo DEF:

T E F = T E = 1000   l b ∙ i n .

T E F = 8   i n .         J E F π 2 d 2 4 = 31,063 × 10 - 3 i n 4

U E F = T E F 2 L E F 2 G J E F = 1000 2 8 ( 2 ) ( 11,2 × 10 6 ) ( 31,063 × 10 - 3 ) = 11,497   l b ∙ i n .

U = U A B + U B C + U D E + U E F = 20,389   i n . ∙ l b

φ A = 2 U T A = 2 20,389 750 = 54,4 × 10 - 3 r a d

φ A = 3,12 °

Resposta

Então gurizada, como acabamos de calcular, temos a resposta de φ A = 3,12 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco de raio a foi soldado à extremidade B do eixo de aço de seção cheia A B . Um cabo é enrolado ao redor do disco e uma força vertical P é aplicada à extremida C do cabo. Sabendo que o raio do e
A barra de aço A B C de 12m m de diâmetro foi dobrada na forma mostrada na figura. Sabendo que E = 200G P a e G = 77,2G P a , determine a deflexão da extremidade C provocada pela força de 150N .
Uma haste uniforme de rigidez à flexão E I é carregada conforme mostrado. Determine ( a ) a deflexão horizontal no ponto D , ( b ) a declividade do ponto D .
A barra de aço CD, com 20mm de diâmetro está soldada ao eixo de aço AB também com 20 mm de diâmetro conforme mostrado. A extremidade C da barra CD toca a superfície rígida mostrada quando um conjugado
Para a viga e carregamento mostrados, (a) calcule o trabalho das forças quando elas são aplicadas sucessivamente à viga, usando o apêndice D , (b) calcule a energia de deformação da viga pelo método d