Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 110

Três hastes, cada uma com a mesma rigidez E I ,   são soldadas para formar o pórtico A B C D . Para o carregamento mostrado, determine a deflexão no ponto D .

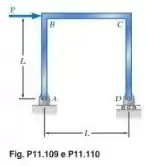
Passo 1

Fala aí, galera. Tudo bem? Bora pra outra questão.

Primeiramente, determinaremos os esforços em alguns pontos:

∑ M A = 0

D L - P L = 0

D = P

∑ F x = 0

- A x + P + Q = 0

A x = ( P + Q )

∑ F y = 0

A y + D = 0

Sabemos que:

U = U A B + U B C + U C D

Passo 2

Primeiro, calcularemos para o membro A B :

M = P + Q y

∂ M ∂ Q = y

Logo, como Q = 0   e M = P y :

U A B = ∫ 0 L M 2 2 E I d y

Logo:

∂ U A B ∂ Q = ∫ 0 L M E I ∂ M ∂ Q   d y = P L 3 3 E I

Fazendo o mesmo para B C :

U B C ∂ Q = P L 3 2 E I

E para o membro C D :

U C D ∂ Q = 0

Passo 3

Logo, basta substituir:

U = U A B + U B C + U C D

U = P L 3 3 E I + P L 3 2 E I + 0

U = 5 P L 3 6 E I

Prontinho, mais uma questão feita!

Resposta

U = 5 P L 3 6 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga prismática mostrada, determine a deflexão no ponto D .
Para a viga prismática mostrada, determine a inclinação em D . Use E = 29 × 10 6p s i .
Para a viga prismática mostrada, determine a inclinação em D . Use E = 29 × 10 6p s i .
Usando as informações no Apêndice D , calcule o trabalho das cargas quando elas estão aplicadas à viga (a) se a força P for aplicada primeiro e (b) se o momento M for aplicado primeiro.
Para a viga prismática mostrada, determine a deflexão em A .