Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 106

Para a barra de seção uniforme e o carregamento mostrados, e usando o teorema de Castigliano, determine a deflexão do ponto B .  

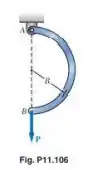
Passo 1

Fala aí, galera. Tudo bem? Bora pra outra questão.

Primeiramente, usando coordenadas polares:

∑ M = 0

P x - M = 0

M = P x = P R s e n φ

Agora, podemos calcular a energia de deformação através de:

U = ∫ 0 L M 2 2 E I d s

U = ∫ 0 π P R s e n φ 2 2 E I R d φ

Logo, resolvendo a integral:

U = π P 2 R 4 E I

Passo 2

O teorema de Castigliano nos diz que:

δ = ∂ U ∂ P

Substituindo:

δ = π P R 3 2 E I

Resposta

δ = π P R 3 2 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga e o carregamento mostrados, determine a deflexão do ponto B . Use E = 200G P a .
Para a viga e o carregamento mostrados, determine a deflexão do ponto D . Use E = 200G P a .
Para a treliça e o carregamento mostrados, determine a deflexão vertical e horizontal do nó C .
Para a viga e o carregamento mostrados, determine a deflexão do ponto B . Use E = 200G P a .
Para a viga e o carregamento mostrados, determine a declividade do ponto A . Use E = 200G P a .