Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 105

Uma barra de seção uniforme com rigidez à flexão E I   é dobrada e carregada conforme mostra a figura. Determine a deflexão vertical do ponto A   e (b) a deflexão horizontal do ponto A .

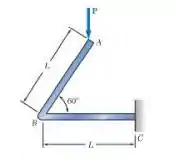
Passo 1

Fala aí, galera. Tudo bem? Bora pra outra questão.

Primeiramente, no trecho A B :

M = 1 2 P v + 3 2 Q v

∂ M ∂ P = 1 2 v

∂ M ∂ Q = 3 2 v

U A B = ∫ 0 L M 2 2 E I d x

Fazendo Q = 0 :

∂ U A B ∂ P = 1 E I ∫ 0 L M ∂ M ∂ P d v = 1 12 P L 3 E I

∂ U A B ∂ Q = 1 E I ∫ 0 L M ∂ M ∂ Q d v = 3 12 P L 3 E I

Para B C :

M = - P x - L 2 + 3 2 Q L

∂ M ∂ P = - x - L 2

U B C = ∫ 0 L M 2 2 E I d x  

Fazendo Q = 0 :

∂ U B C ∂ P = 1 E I ∫ 0 L M ∂ M ∂ P d x = 1 12 P L 3 E I

∂ U B C ∂ Q = 1 E I ∫ 0 L M ∂ M ∂ Q d x = - 3 P 4 E I   x - L 2 2 = 0

Passo 2

Portanto, basta substituir os valores. A deflexão vertical em A :

δ V = ∂ U A B ∂ P + ∂ U B C ∂ P = P L 3 6 E I

A deflexão horizontal no ponto A :

δ H = ∂ U A B ∂ Q + ∂ U B C ∂ Q = 0,144 P L 3 E I

Resposta

  1. δ V = P L 3 6 E I
  2. δ H = 0,144 P L 3 E I
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga e o carregamento mostrados, determine a deflexão do ponto C . Use E = 200G P a .
Para a viga e o carregamento mostrados, determine a inclinação na extremidade A . Use E = 200G P a .
Para a treliça e o carregamento mostrados, determine a deflexão vertical e horizontal do nó C .
Para a treliça e o carregamento mostrado, determinar a energia de deformação
Determinar a reação no apoio móvel e desenhar o diagrama de momento fletor, para a viga com o carregamento indicado.