Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 91
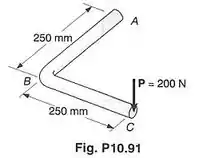
Uma barra de aço de de diâmetro foi dobrada como mostrado. Usando o método do trabalho e energia, determinar a deflexão na extremidade , devida à força de . Usar e .
Passo 1
Oi, pessoas! Como estão? Bora entender método de trabalho e energia através dessa questão?
Essa questão mostra uma barra (que pode ser dividida em uma parte e outra ) sendo carregada com uma força . Essa força faz a parte sofrer flexão e a barra sofrer torção e flexão. O enunciado quer saber quanto vale a deflexão na extremidade devido à força . A figura abaixo mostra o diagrama de corpo livre das duas partes da barra .
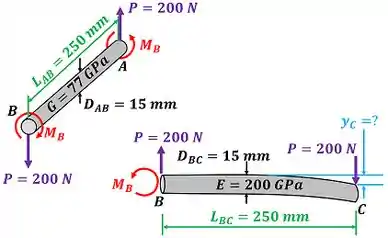
O enunciado quer que a gente calcule através do método de trabalho e energia. Isso quer dizer que achamos , usando duas equações para calcular a energia total que e absorvem. A primeira equação, calcula a partir da força . Dessa forma, conseguimos deduzir uma equação para .
A segunda equação, calcula , somando a energia absorvida pela parte com a energia absorvida pela parte .
Para calcular usamos a equação do exemplo 10.3 do livro que calcula justamente a energia de uma barra que sofre flexão por conta de uma força e usamos a equação 10.22 do livro que calcula a energia absorvida por um eixo em torção que sofre com um torque . Ou seja, é a soma de dois termos. Um relativo à flexão e outro relativo à torção.
Para calcular usamos a equação do exemplo 10.3 do livro que calcula justamente a energia de uma barra que sofre flexão por conta de uma força .
Agora que temos todas essas fórmulas, vamos começar a fazer as contas, calculando o valor dos momentos de inércia e de e de respectivamente e do momento polar da parte .
Passo 2
Achamos através da fórmula de momento de inércia polar para áreas circulares abaixo. Antes, devemos converter o diâmetro de pra , multiplicando eles por .
Encontramos e através da fórmula do momento de inércia para áreas quadrangulares abaixo.
Agora temos que achar o momento para conseguir encontrar !
Passo 3
Calculamos o momento , fazendo o equilíbrio de momentos da parte no ponto . Como o momento da força tende a fazer girar no senti horário, colocaremos um sinal de menos na frente dele. O equilíbrio de momento diz que a soma dos momentos e (momento da força ) deve valer zero. Logo:
No entanto, é a força multiplicada pelo braço de alavanca que vale se convertermos seu valor de pra .
Substituímos os dados nas equações de e para achar as energias de deformação. No entanto, antes disso converter o e o de para , multiplicando e por .
Somando com , achamos .
Substituindo esse valor na fórmula de , achamos:
Feshoooow! Acabamos a questão! Agora é só partir pro abraço! :)