Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 122

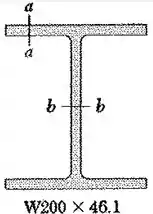
Uma barra de aço com 2438 mm de comprimento e seção transversal W 200 × 46,1 está submetida a um toriqe de 565 N.m. As propriedades da seção laminada são dadas no apêndice C. Sabendo que G = 77,2 GPa, determine (a) a tensão de cisalhamento máxima ao longo da linha a-a, (b) a tensão de cisalhamento máxima ao longo da linha b-b e (c) o ângulo de torção. (Sugestão: considere a alma e as mesas separadamente e obtenha uma relação entre os torques aplicados na alma e na mesa, respectivamente, mostrando que os ângulos de torção são iguais.)

Passo 1

Observando a seção transversal, temos duas regiões, a “flange” e a “web”.

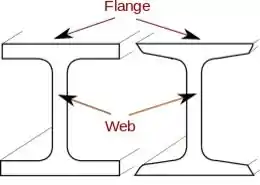
Para a flange temos (a partir do apêndice c):

a = 203   m m  

b = 11   m m

A relação de a e b por

a b = 2 03 11 = 18,45

Como essa relação é maior que 5, não usaremos a tabela 3.1 e sim usaremos a relação abaixo para determinaor c 1 e c 2

c 1 = c 2 = 1 3 1 - 0,630 b a = 1 3 1 - 0,630 × 11 203 = 0,3 22 0

Temos ainda a relação

ϕ F = T F L c 2 a b 3 G

Isolando T F

T F = c 2 a b 3 G ϕ F L = 0,322 0,203 0,011 3 G ϕ F L = 87 × 10 - 9 × G ϕ F L

Passo 2

Para a parte da web nós teremos

a = 203 - 2 11 = 181   m m

b = 7,2   m m

A relação entra a e b então é

a b = 181 7,2 = 25,14

Como essa relação é maior que 5, não usaremos a tabela 3.1 e sim usaremos a relação abaixo para determinaor c 1 e c 2

c 1 = c 2 = 1 3 1 - 0,630 b a = 1 3 1 - 0,630 × 7,2 181 = 0 , 3249

Temos ainda a relação

ϕ w = T w L c 2 a b 3 G

Isolando T F

T w = c 2 a b 3 G ϕ w L = 0,32 49 0 , 181 0,0 72 3 G ϕ w L = 21,95 × 10 - 9 × G ϕ w L

Passo 3

Bom, agora que temos esses dados, temos ainda que garantir que o ângulo de rotação seja igual em todas as partes, certo? Então

ϕ F = ϕ w = ϕ

Temos ainda também que o torque total vai ser dado por

T = 2 T F + T w = 2 × 87 × 10 - 9 × G ϕ L + 21,95 × 10 - 9 × G ϕ L = 1,9595 × 10 - 7 × G ϕ L

Temos então que

T = 1,9595 × 10 - 7 × G ϕ L → G ϕ L = T 1,9595 × 10 - 7 = 560 1,9595 × 10 - 7 = 2,85 × 10 9

G ϕ L = 2,85 × 10 9

Lembra la do começo que temos que

T F = 87 × 10 - 9 × G ϕ L = 248,6   N . m

T w = 21,95 × 10 - 9 × G ϕ L = 62,7   N . m

Com isso tudo podemos partir pra o que cada questãozinha pede.

Passo 4

a) tensão de cisalhamento máxima ao longo da linha a-a.

τ F = T F c 1 a b 2 = 248,6 0,3219 0,203 0,011 2 = 31,44   M P a

b) a tensão de cisalhamento máxima ao longo da linha b-b

τ w = T w c 1 a b 2 = 62,7 0,3249 0,181 0,0072 2 = 20,57   M P a

c) o ângulo de torção

G ϕ L = 2,85 × 10 9

ϕ = L × 2,85 × 10 9 × 1 G = 2,438 × 2,85 × 10 9 × 1 77 × 10 9 = 0,0902   r a d

0,0902 → ϕ

π → 180

ϕ = 5,17 °

Resposta

a )   τ F = 31,44   M P a

b )   τ w = 20,57   M P a

c )   ϕ = 5,17 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixos A e B são feitos do mesmo material e têm a mesma área de seção transversal, mas A tem uma seção transversal circular e B tem uma seção transversal quadrada. Determine a relação dos torques máx
O eixos A e B são feitos do mesmo material e têm o mesmo comprimento e a mesma área de seção transversal, mas A tem uma seção transversal circular e B tem uma seção transversal quadrada. Determine a r
Um torque de 4 kN.m é aplicado a um perfile cantoneira L 203 × 203 × 25,4 de aço, cuja espessura da seção é 25,4 mm e a área da seção transversal de 9680 mm², codorme apêndice C. Sabendo-se que G = 77
Uma barra de aço com 3 m de comprimento e seção transversal W 25 0 × 58 . Sabendo que G = 77,2G P a , e que a tensão de cisalhamento admissível é de 35 MPa, determine (a) o maior torque T que pode ser
Uma cantoneira de aço com 3 m de comprimento tem seção L 203 × I 52 × 12,7m m . Obtém-se do Apêndice C que sua espessura é de 12,7 mm e que a área de sua seção transversal é 4350 mm². Sabendo que τ a