Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 120

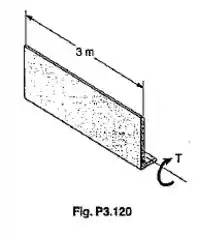
Uma cantoneira de aço com 3 m de comprimento tem seção L 203 × I 52 × 12,7   m m . Obtém-se do Apêndice C que sua espessura é de 12,7 mm e que a área de sua seção transversal é 4350 mm². Sabendo que τ a d m = 50   M P a   e que G = 77 GPa, e ignorando o efeito da concentração de tensões, determine (a) o maior toruqe T que pode ser aplicado e (b) o correspondente ângulo de giro.

Passo 1

Dessa questão temos

A = 4350   m m 2  

b = 12,7   m m

τ a d m = 50   M P a

G = 77 × 10 9   P a

Inicialmente a questão nos pede o maior torque T. Temos a relação

τ a d m = T c 1 a b 2

Passo 2

Precisamos então descobrir o valor de c 1   e a .   Para a temos que a = A b

a = A b = 4350 12,7 = 342,52   m m

Temos então que

a b = 342,52 12,5 = 26,97

Como essa relação é maior que 5, pela teoria temos que c 1 e c 2 serão dados por

c 1 = c 2 = 1 3 1 - 0,630 b a = 1 3 1 - 0,630 × 12,7 342,52 = 0,32555

Passo 3

a) Já podemos então descobrir o valor de T

τ a d m = T c 1 a b 2 → T = c 1 a b 2 τ a d m = 0,32555 342,52 × 10 - 3 12,7 × 10 - 3 2 50 × 10 6

T = 89 9,25   N . m

Passo 4

b) Para o cálculo do ângulo vamos usar a outra relação

ϕ = T L c 2 a b 3 G = 899,25 3 0,32555 342,52 × 10 - 3 12,7 × 10 - 3 3 77 × 10 9 = 0,15339   r a d

Transformando de radianos para grau

180 → π

ϕ → 0,1539

ϕ = 8,79 °

Resposta

a )   T = 89 9,25   N . m

b )   ϕ = 8,79 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada uma das três barras de aço mostradas na figura está submetida a um torque de intensidade T = 565 N.m. Sabendo que a tensão de cisalhamento admissível de 55 MPa, determine a dimensão b necessária
Cada uma das três barras de aço mostradas na figura deve ser girada por um ângulo de 2 ° . Sabendo que b=30 mm, τ a d m = 50M P a , e G=27 GPa, determine o menor comprimento admissível para cada barra
Cada uma das três barras de aço mostradas na figura deve ser girada por um ângulo de 1,25 ° . Sabendo que b=38 mm, τ a d m = 50M P a , e G=26 GPa, determine o menor comprimento admissível para cada ba
O eixos A e B são feitos do mesmo material e têm a mesma área de seção transversal, mas A tem uma seção transversal circular e B tem uma seção transversal quadrada. Determine a relação entre as máxima
O eixos A e B são feitos do mesmo material e têm o mesmo comprimento e a mesma área de seção transversal, mas A tem uma seção transversal circular e B tem uma seção transversal quadrada. Determine a r