Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 123
Uma barra de aço com 3 m de comprimento e seção transversal . Sabendo que , e que a tensão de cisalhamento admissível é de 35 MPa, determine (a) o maior torque T que pode ser aplicado e (b) o ângulo de torção correspondente. Ver no Apêndice C as dimensões da seção transversal e despreze o efeito das concentrações de tensão. (Ver a sugestão do Problema 3.122).
Passo 1
Observando a seção transversal, temos duas regiões, a “flange” e a “web”.
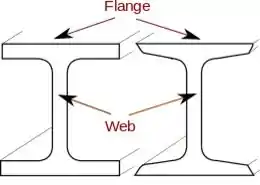
Para a flange temos (a partir do apêndice c):
A relação de a e b por
Como essa relação é maior que 5, não usaremos a tabela 3.1 e sim usaremos a relação abaixo para determinaor e
Temos ainda a relação
Isolando
Passo 2
Para a parte da web nós teremos
A relação entra a e b então é
Como essa relação é maior que 5, não usaremos a tabela 3.1 e sim usaremos a relação abaixo para determinaor e
Temos ainda a relação
Isolando
Passo 3
Bom, agora que temos esses dados, temos ainda que garantir que o ângulo de rotação seja igual em todas as partes, certo? Então
Temos ainda também que o torque total vai ser dado por
Temos então que
Lembra la do começo que temos que
Passo 4
Para determinarmos o valor de , como temos o valor da tensão de cisalhamento admissível, podemos usar a relação
Então o T que a Flange aguenta será
Já para a Web é
Então o T máximo que pode ser aplicado é de 924,6, pos caso seja superior, a Flange não suporta. Tranquilo??
Passo 5
A questão ainda nos pede o ângulo de torção correspondente. O ângulo nos é dado pela relação que descobrimos no passo 3.
Transformando para grau