Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 103
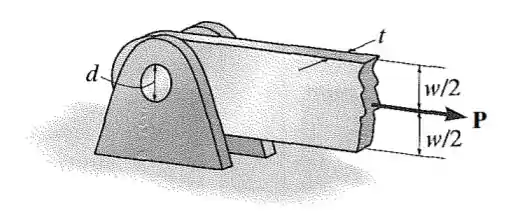
A barra é suportada pelo pino. Se a tensão de tração admissível para a barra for e a tensão de cisalhamento admissível para o pino for , determine o diâmetro do pino para o qual a carga será máxima. Qual é essa carga máxima? Considere que o orifício na barra tem o mesmo diâmetro d do pino. Considere também .
Passo 1
Oláaaaa, querido! Tá bem?
Então, a gente quer encontrar o diâmetro do pino que implica na carga sendo máxima e, para isso, devemos relacionar esses valores que desejamos encontrar com as equações que regem as tensões admissíveis, já que elas foram dadas no problema, sacou?
A expressão da tensão normal máxima que pode atuar na barra é
Essa força é a força normal mostrada na figura e é a área da menor seção transversal da barra (já que queremos máximo). Percebe que a barra tem um buraco por causa do parafuso.
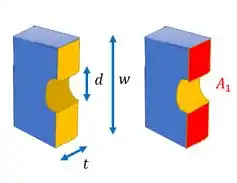
Então a menor seção transversal é a seção que passa pelo meio do parafuso, ou seja, onde o buraco da barra tem a altura do diâmetro do parafuso. Por isso vale
E a tensão de cisalhamento é
Onde é a força resultante de cisalhamento num parafuso e a área da seção circular dele:
Passo 2
Dadas as equações acima podemos montar um sisteminha que relacione e . Vamos começar pela tensão normal:
Substituindo os valores do enunciado:
Passo 3
No caso do cisalhamento, nós vamos ter cisalhamento duplo porque a força é transmitida para o parafuso pela barra. E o parafuso transmite essa força a base por duas placas (uma de cada lado). A presença dessas duas placas é o que indica para gente o cisalhamento duplo.
Logo a nossa força vai ser dividida por 2 na equação da tensão de cisalhamento, assim
Passo 4
Temos essas duas equações:
Temos o valor de todas as letrinhas, menos e que queremos descobrir.
Então, substituindo os dados e resolvendo o sistema de equações composto pelas equações e vamos encontrar