Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 73
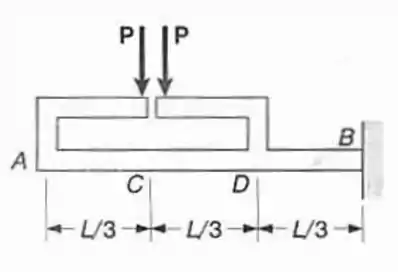
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar o máximo momento fletor no ponto B.
Passo 1
Agora a gente vai resolver os problemas com a utilização de funções singulares, mas o que é isso? Olha a função abaixo:
Esse é uma função normal, correto? Mas imagina que eu quero fazer o seguinte: Ignorar o segundo termo quando . Nós podemos fazer escrevendo:
Dessa forma vamos admitir duas hipóteses:
Quando a função fica:
Quando a função fica:
Legal né? É essa propriedade que vamos utilizar neste problema.
Passo 2
Vamos calcular as reações nos pontos e . Para isso vamos fazer o somatório das forças em igual a zero (é um problema de estática, lembre-se):
Perceba que a barra está engastada em , desta forma, teremos duas reações (uma horizontal e uma vertical) mais um momento puro chamado .
Como só existe uma força em então nem precisamos fazer nenhuma conta .
Já para temos:
Para o momento, sempre aplicado em conforme pede o livro.
Passo 3
Agora o importante é achar a função singular que define o carregamento, nesse caso será:
Perceba que não existe carregamento distribuído.
“Ah e as forças e o momento puro?” Serão contabilizados nos passos seguintes =D
Passo 4
Agora a gente vai integrar essa função em de modo a achar o vetor cortante :
Aqui é importante notar que a constante é igual à força de reação. Mas a única força de reação está no final da barra, então não vai ser contabilizada. Assim a constante é igual apenas as duas forças
O que faz sentido né? Antes do ponto a força cortante é nula e após é igual a .
Passo 5
Para achar o momento fletor basta que a gente integre novamente =D
A constante é igual a qualquer momento puro, mas como só existe no final da barra não faz sentido colocar. Olha só porque:
Esse valor só vai ser diferente de zero quando , ou seja, num único ponto! Para nós isso não vai fazer diferença. Então:
Passo 6
Para achar o momento fletor em basta substituir na equação:
Resposta
a)
b)