Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas Revisão - Ex. 136
Uma barra de alumínio AB (G=26 GPa) é ligada a uma barra de latão (G=39 GPa). Sabendo-se que o trecho CD da barra é vazado e tem um diâmetro interno de 40 mm, determinar o ângulo de torção em A.
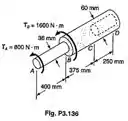
Passo 1
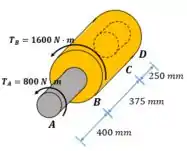
A primeira coisa que faremos é calcular a reação em
Agora vamos analisar a distribuição de torque ao longo do eixo. No ponto A é aplicada uma torção de 800 Nm anti-horária. Assim, a torção entre o ponto A e B é:
No ponto B são adicionados mais 1600 Nm anti-horários.
No ponto C não é adicionado nenhum torque, ou seja, o torque se mantém o mesmo:
Passo 2
Agora vamos calcular os momentos de inércia polar nas diferentes regiões:
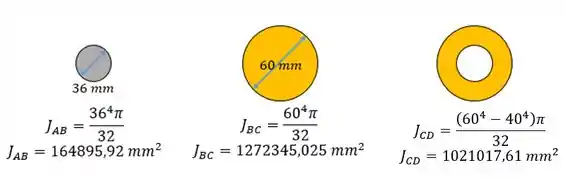
Passo 3
O ponto está engastado, então o ponto não sofrerá nenhuma deformação. Ele será nossa referência.
Então a deformação do ponto A em relação ao ponto D será: