Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 107
O tubo simétrico é feito de aço de alta resistência, tem as dimensões médias mostradas na figura e de espessura. Se for submetido a um torque , determine a tensão de cisalhamento média desenvolvida nos pontos A e B. Indique a tensão de cisalhamento em elementos de volume localizados nesses pontos.
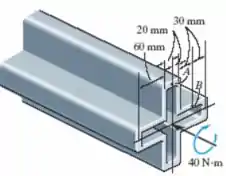
Passo 1
Fala, meu jovem! Ele deu um tubo não circular e pede a tensão de cisalhamento nos pontos A e B.
Aqui temos uma típica questão de tubos de paredes finas. O segredo para resolver esse bonito é usar a fórmulnha:
Onde é o nosso torque de . é a área média da seção. E é a espessura da parede do tubo no ponto onde a gente quer calcular a tensão.
Percebe que para e , essa expessura é a mesma, . Então essas tensões serão iguais. O que pode mudar vai ser seus sentidos.
Vamos montar essa fórmulinha e partir para o abraço!
Passo 2
O problema já nos dá as dimensões médias, podemos calcular a área média sem nos procuparmos com a espessura.
Observando a imagem abaixo, vamos calcular a área média:
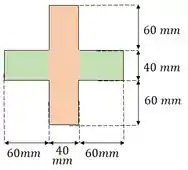
Passo 3
Agora, basta aplicar a Equação 5.18.
Para o ponto A:
Vamos converter as unidades e deixar tudo em milímetros:
E sabemos que :
Como :
Percebeu? Nesse a Equação 5.18 não se importa com a posição do ponto! Em qualquer lugar da viga, a tensão será a mesma.
Passo 4
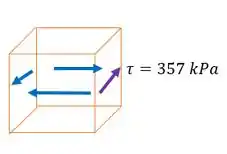
Agora vamos desenhar os elementos de volume. O sentido da tensão em cada ponto da seção vai ser o sentido do torque ao passar por ele. E as outras setinhas do elemento só são para garantir o equilíbrio dele.
Temos algo assim:
Ih até os sentido são iguais. Então vamos fazer um elemento só que serve para os dois:
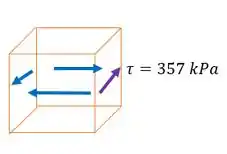
Resposta
