Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 104
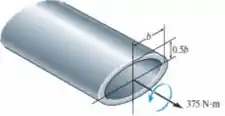
O tubo de aço tem seção transversal elíptica com as dimensões médias mostradas na figura e espessura constante . Se a tensão de cisalhamento admissível para e o tubo tiver de resistir a um torque determine a dimensão . A área média para a elipse é .
Passo 1
Para resolver a questão, basta aplicar a Equação 5.18
Organizando a equação:
Lembrando das unidades de medida, sabemos que
Resposta
Exercícios de Livros Relacionados
O tubo simétrico é feito de aço de alta resistência, tem as dimensões médias mostradas na figura e 5m m de espessura. Se for submetido a um torque T = 40N ⋅ m , determine a tensão de cisalhamento médi
Para um tensão de cisalhamento média dada, determine o fator de elevação da capacidade de resistência a torção se as seções semicirculares dorem invertidas das posições indicadas pelas linhas tracejad
O tubo é feito de plástico, tem 5mm de espessura e as dimensões médias são mostradas na figura. Determine a tensão de cisalhamento média nos pontos A e B se o tubo for submetido a um torque T = 500N ⋅
O tubo de aço tem seção transversal elíptica de dimensões médias mostradas na figura e espessura constante de t = 5 m m . Se a tensão de cisalhamento admissível for τ a d m = 56M P a , determine a dim
Para uma dada tensão de cisalhamento máxima, determine o fator de elevação da capacidade de resistência ao torque se a seção semicircular for invertida da posição indicada pela linhas tracejadas para