Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 109
Para um tensão de cisalhamento média dada, determine o fator de elevação da capacidade de resistência a torção se as seções semicirculares dorem invertidas das posições indicadas pelas linhas tracejadas para as posições da seção mostrada na figura. O tubo tem espessura de
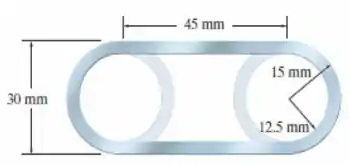
Passo 1
Analisando o enunciado, vamos ter que trabalhar com duas geometrias e comparar o torque máximo que pode atuar em cada uma delas.
Passo 2
Vamos calcular as medidas da região media (pontilhada na figura anterior):
Passo 3
Para aplicarmos a equação da torção precisamos calcular a área média, expressa em laranja na figura:
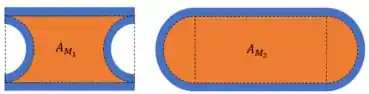
Passo 4
Em posse das áreas, podemos correlacionar os torques que atuam em cada uma delas. Lembrando da equação 5.18:
Podemos reorganizar a equação em função do torque:
Em uma análise da equação acima, percebemos que se a tensão de cisalhamento e a espessura forem constantes, então a geometria que tiver a maior área, terá o maior torque.
Passo 5
Para obter uma proporção entre os torques das geometrias, vamos divir o torque de uma pela da outra: