Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 135
Para a barra e o carregamento do , determinar a variação dos valores da largura para que a tensão no ponto A seja de tração e igual ou menor que
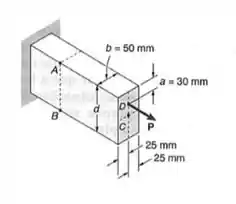
Passo 1
Para podermos determinar a largura da barra afim de termos a tensão do ponto A máxima, precisamos definir a tensão na barra em função do que temos, sendo assim, temos que lembrar que a tensão na barra tem que ser definida da seguinte maneira.
Sabemos que:
Em que é a excentricidade da carga com relação ao centroide da seção. Com isso temos que:
Sabemos também que:
Substituindo teremos que:
Passo 2
Se queremos que seja tensão de tração, sabemos que tem que ser acima de 0, e também temos que garantir que seja baixo de , com isso teremos que:
Resolvendo a primeira metade, teremos que:
Resolvendo a outra metade, teremos que:
como queremos apenas ter os valores positivos, teremos que:
Juntando tudo que temos, podemos definir que:
E
Que são as variações dos valores de que permitem que a tensão seja só de tração, porém abaixo de .
Resposta
E