Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 108
Para a barra composta do , determinar a tensão residual em cada porção da barra, se cresce gradualmente desde zero até e então decresce até zero.
Passo 1
O enunciado nós da os seguintes dados sobre o nosso problema
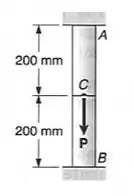
Agora precisamos fazer duas coisas para resolver o nosso problema, que é definir a tensão residual do nosso problema, que é usar a equação de equilíbrio e usar a fórmula de compatibilidade, sendo assim teremos que:
- Equação de equilíbrio
- Equação de compatibilidade
A equação de equilíbrio é dada por:
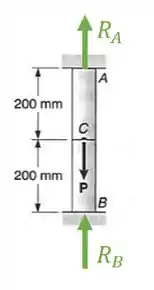
Assim a fórmula será dada por:
Mas não conseguimos determinar os valores por essa fórmula, por isso temos que usar a nossa equação de compatibilidade, então o nosso primeiro passo é supor que o nosso problema seja elástico, e sabendo dessa informação, calculamos as tensões, e a que ultrapassar o valor usaremos como base para calcular a tensão residual, com isso vamos ter o seguinte:
Sabemos que o somatório de deformações totais nesse trecho tem que ser zero. Com isso teremos que:
E sabemos que:
E sabemos que:
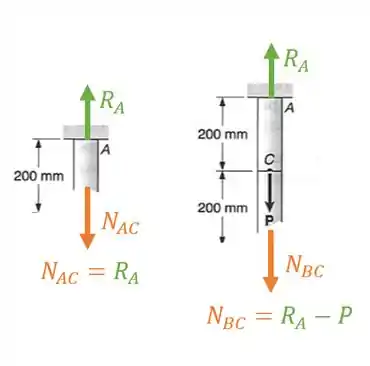
Substituindo os normais teremos que:
Substituindo teremos que:
Definindo os normais teremos que:
Calculando a tensão teremos que:
Sabemos que a máxima tensão que a barra AC suporta é de , como temos uma tensão de agindo, isso seria impossível, ou seja, temos deformações plásticas ocorrendo na nossa estrutura e a tensão que iremos considerar que de fato age na nossa barra é a máxima que ela suporta, ou seja, vamos definir essa tensão como a tensão real que será dada por:
E para a barra BC teremos que:
E para a barra BC, não teremos o mesmo problema, porque a sua tensão admissível é dada por , como a tensão que age é dada por , podemos manter ela como a tensão real que age na barra BC.
E assim finalizamos o nosso passo 1.
Passo 2
Como sabemos quais são as tensões reais, e como sabemos que a barra AC vai ter deformações elásticas, podemos definir que a nova equação de compatibilidade (que continua tendo deformação total igual a zero) deverá ter uma parcela de deformação elástica que será dada por:
E aqui vai um macete legal para podermos facilitar as contas, sabemos que:
Mas precisamos da tensão para podermos substituir, com isso podemos fazer a seguinte conta:
E basicamente fizemos . Fazendo o mesmo com a outra barra teremos que:
Substituindo na fórmula teremos que:
Como o objetivo é determinar a deformação plástica temos que:
substituindo os valores teremos que:
E a tensão residual será calculada pelo seguinte cálculo:
Assim a tensão residual será dada por: