Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 118
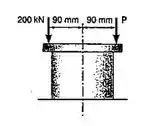
4.118 - As duas forças mostradas são aplicadas a uma placa rígida, suportada por um tubo de aço de de diâmetro externo e de diâmetro interno. Sabendo-se que a tensão admissível compressiva é de , determinar a variação de valores admissíveis para .
Passo 1
A primeira coisa que devemos fazer aqui é determinar os esforços internos na seção do tubo devido a aplicação das duas forças na placa.
Na seção, vamos ter a ação direta da força de valor igual a mais :
E além dele, temos o momento fletor causados pelas forças aplicadas fora das laterias do tubo (o diâmetro externo te raio igual a , e as forças são aplicadas a do dentro de flexão):
Onde significa () e é ():
Descobertos esses valores, simbora para o passo 2!
Passo 2
Nesse passo, temos que buscar as informações que dependem da geometria do problema, como os valores da área da seção transversal e momento de inércia:
A área da seção vai ser a área desse círculo maior de raio menos a área do círculo menor ( de raio):
Essa área está em , ok?
MOMENTO DE INÉRCIA:
Para o momento de inércia com relação ao eixo de simetria, devemos calcular o momento de inércia do círculo maior e depois subtrair pelo momento de inércia do círculo menor:
- Círculo maior
- Círculo menor
Portanto o momento de Inércia de toda a seção será...
Passo 3
Agora podemos buscar as tensões de compressão pela força que gera uma distribuição uniforme de trações:
Sabemos que o momento , causa uma distribuição linear de tensões. Na compressão...
Onde vale a distância de um dos lados extremos da seção até o centro neutro...
Portanto nada mais é do que o raio externo...
Então...
Passo 4
Agora vamos avaliar os casos possíveis já que sabemos que a maior tensão admissível é:
Então a máxima compressão possível é no extremo...
Como isso não pode ultrapassar ...
Ou, por ooutro lado, também pode não ter força nenhuma:
Gerando um limite então...
Mas ainda podemos ter o caso...
Ou ainda...
Nesse caso...
Olhando as duas faixas que a gente obteve agora, a faixa admissível é...