Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 117
Três barras do mesmo material e mesma área são usadas para suportar a força Determine o esforço na barra
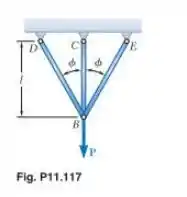
Passo 1
Fala aí, galera. Tudo bem? Bora pra outra questão.
Primeiramente, sabemos que a energia de deformação é dada por:
O deslocamento, é dado por:
No nó temos que:
No nó
Juntando as equações:
Passo 2
Agora, vamos calcular alguns parâmetros e tabelar, para ajudar a gente.
Por fim, basta substituir na fórmula do deslocamento:
Logo:
Resposta
Exercícios de Livros Relacionados
Um amortecedor de vibrações consiste em dois blocos de borracha, com um módulo de elasticidade transversal G = 19M P a , colocados à placa A B , e dois suportes rígidos. Expressando por P a intensidad
Determine a dilatação e e a variação em volume do segmento de 200 mm da barra mostrada se (a) abarra fosse feita de aço com E = 200G P a e v = 0,3 e (b) a barra fosse feita de alumínio com E = 70G P a
Para o apoio de elastômero do Prblema 2.81 com b = 22 0 m m e a = 30m m , determine o módulo de cisalhamento G e a tensão de cisalhamento τ para a força lateral máxima P = 19k N e um deslocamento máxi
Dois blocos de borracha com um módulo de elasticidade transversal G = 12M P a são colocados aos suportes rígidos e à placa A B . Sabendo-se que c = 100m m e P = 45k N , determine as menores dimensões
Um suporte isolado de vibrações consiste em uma barra A de raio R 1 = 10m m e um tupo B de raio interno R 2 = 25m m , colado a um tubo de borracha de 80 mm de comprimento com um módulo de elasticidade