Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 18
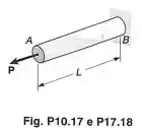
Uma barra de de diâmetro, com comprimento é feita de uma liga de alumínio para a qual e . Sabendo-se que uma energia de deformação de deve ser absorvida pela barra assim que a carga axial é aplicada, determinar o coeficiente de segurança da barra com relação à deformação permanente.
Passo 1
Faaaala, lindezas! Partiu fazer uma questão de energia de deformação?
O enunciado quer que a gente calcule o coeficiente de segurança que evita a barra de se deformar permanentemente. Esse coeficiente é igual à energia da barra de quando ela está prestes a se deformar permanentemente dividida pela energia que a barra tem, quando está sob carga .
Nós já temos . Logo, para calcular precisamos achar apenas .
A imagem abaixo mostra os dados que precisamos para achar .
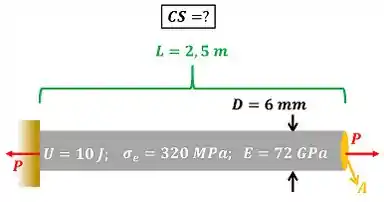
é a área da seção transversal da barra. é o diâmetro da barra. é o módulo de elasticidade da barra. é o comprimento da barra. é a máxima tensão que a barra pode sofrer sem se deformar permanentemente.
Para achar a energia que faz barra se deformar permanentemente, precisamos achar a carga que causa essa deformação. Essa carga é igual à tensão vezes .
Para calcular a energia de deformação a partir da força precisamos usar a equação 10.14 do livro. Esse equação é válida para barras com áreas da seção transversal constantes, como é o nosso caso!
Agora que temos todas essas informações em mãos, vamos calcular o coeficiente de segurança da barra nos próximos passos!
Passo 2
Nesse passo nós vamos calcular a área em , além de calcular o valor de em newton .
Primeira etapa cumprida! Vamos achar a força agora!
Mas antes, temos que lembrar que a tensão admissível vale .
Passo 3
Agora sim estamos prontos para calcular e !
No entanto, ainda temos que converter de para , multiplicando por .
Sabendo disso, somos capazes de achar .
Substituindo esse valor na fórmula de , achamos:
Uhuuuul! Questão feita! Mandou muito bem!