Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 79
Dois blocos de borracha com um módulo de elasticidade transversal são colocador a dois suportes rígidos e a uma placa AB. Sabendo que , determine as menores dimensões admissíveis dos blocos para que a tensão de cisalhamento na borracha não exceda 1,4 MPa e o deslocamento da placa seja no mínimo de 4,8mm.
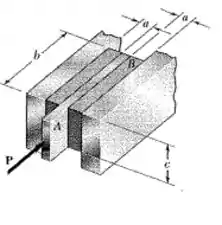
Passo 1
Para começar vamos anotar os dados que nós temos:
Representados abaixo temos a vista superior dos blocos
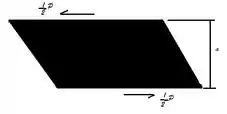
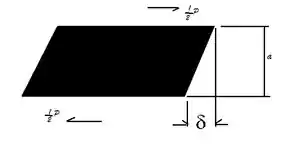
Passo 2
Para nossos cálculos teremos então
Onde é a tangente referente à variação do ângulo. Isso faz com que a força seja proporcional ao deslocamento relativo.
Logo para determinarmosa medida de temos
Passo 3
Para podermos relacionar o temanho de a e b, podemos usar a relação a partir de
Isolando então b temos
Resposta
Exercícios de Livros Relacionados
Um suporte isolado de vibrações consiste em uma barra A de raio R 1 e um tupo B de raio interno R 2 , colado a um tubo de borracha de 80 mm de comprimento com um módulo de elasticidade transversal G =
As constantes de matéria E, G, k e v estão relacionadas nas equações (2.33) e (2.43). Mostre que qualquer uma dessas constantes pode ser expressa em função de quaisquer outras duas constantes. Por exe
Sabendo-se que a tensão normal admissível para o aço da barra mostrada vale 150 MPa, determinar a máxima força P admissível, axial e centrada, que pode ser aplicada à barra.
O cubo do problema 2.89, de um material compósito, é impedido de se deformar na direção z e é alongado na direção x em 0,035 mm por uma força de tração na direção x. Determine (a) as tensões σ x , σ y
O corpo de prova de alumínio mostrado é submetido a duas forças centradas e axiais iguais e opostas, de intensidade P. Pede-seSabendo-se que E=70GPa e σ a d m = 200 M P a , determinar o máximo valor a