Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 85
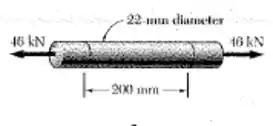
Determine a dilatação e a variação em volume do segmento de 200 mm da barra mostrada se (a) abarra fosse feita de aço com e e (b) a barra fosse feita de alumínio com e
Passo 1
Vamos começar calcuando a área da seção circular
Já que o enunciado já nos passou , podemos aplicar a relação
Como não temos forças presentes em y e z temos
Passo 2
Para calcularmos a dilatação fazemos
Para o volume teremos
Passo 3
Com tudo isso em mão podemos finalmente comçar a calcular o que as questões pedem.
a) Para o aço
b) Para o alumínio
Resposta
a) Para o aço
b) Para o alumínio
Exercícios de Livros Relacionados
Uma barra cilíndrica A B tem um comprimento L de 1,50m e um diâmetro de 20m m . Ela é feita de um aço doce, que é assumido ser elastoplástico com E = 200G P a e σ e = 250M P a . Uma força P é aplicada
A barra AB consiste em duas porções, AC e CB, cada uma com 200 mm de comprimento e 1935m m 2 de área da seção transversal. A porção AC é feita de um aço doce com E = 200G P a e σ 2 = 250M P a , a porç
A barra AB consiste em duas porções, AC e CB, cada uma com 200 mm de comprimento e 1935m m 2 de área da seção transversal. A porção AC é feita de um aço doce com E = 200G P a e σ 2 = 250M P a , a porç
Para a barra composta do Problema 2.104, se P cresce gradualmente desde zero até a deflexão do ponto C atingindo um valor máximo σ m e depois retorna a zero, pede-se determinar o máximo valor de P, a
Para a barra composta do Problema 2.104, se P cresce gradualmente desde zero até a deflexão do ponto C atingindo um valor máximo σ m e depois retorna a zero, pede-se determinar o máximo valor de P, a