Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 155
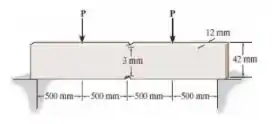
A barra entalhada simplesmente apoiada é submetida a duas forças P. Determine o maior valor de P que pode ser aplicado sem provocar o escoamento do material. O material é aço A-36. Cada entalhe tem raio r = 3 mm
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que essa barra doidona aí tem duas forças aplicadas de forma equidistante de seus apoios de momento, e nos pede a própria força, para que o aço continue intacto. Nem parece tão difícil, é só a gente olhar para aquele ponto lá de cima e fazer. Partiu??
Passo 2
Nosso primeiro passo vai ser fazer o DCL e achar a relação entre o momento e a nossa força aplicada.
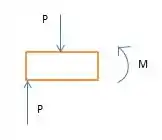
Agora, precisamos achar nossas relações entre a espessura () e a altura média com a altura relativa ao ponto de momento (, que vai ser bem naquele estreitamento. Da nossa relação , teremos nosso fator de concentração de tensão (K).
Passo 3
Pronto!! Agora vamos jogar tudo lá na nossa formulinha e teremos a nossa força máxima.