Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 142
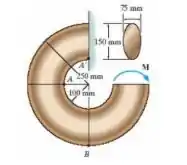
O elemento tem seção transversal elíptica. Se a tensão de flexão admissível for σadm = 125 MPa, determine o momento máximo M que pode ser aplicado ao elemento.
Passo 1
Faaaala, meu povo bonito!! Tudo bem com vocês?? A nossa questãozinha nos mostra essa peça de três quartos de circunferência e nos pede para calcular o valor do momento máximo para que a tensão admissível não seja ultrapassada. Viu?? Ela só tem cara de malvada, mas vamos resolver rapidinho. Vem comigo!!
Passo 2
Nosso primeiro passo será calcular a área e o r’.
A = π x 75 x 37,5 =8835,7293 mm²
r’ = 100 + 75 = 175 mm
Feito isso, precisamos determinar a localização do centroide, que é medida em ação ao centro de curvatura, seguido pelo cálculo do eixo neutro. Como nossa estrutura pode ser dividida em vários pedacinhos com partes compostas, podemos integrar tudo.
= 53,049 mm
R = = = 166,55694 mm
Passo 3
Pronto, nossos pontos mais difíceis da questão já foram resolvidos. Só falta calcularmos as tensões em cada extremidade do corte.
σa =
M = 14 kN.m
σb =
M = 27,94 kN.m
Resposta
M = 14 kN.m