Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 4
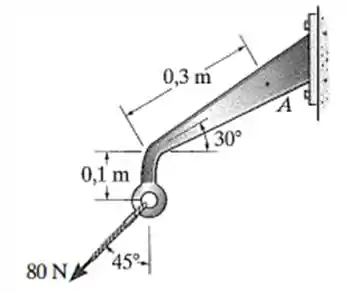
O dispositivo mostrado na figura sustenta uma força de . Determine as cargas internas resultantes que agem sobre a seção no ponto .
Passo 1
Fala aí galerinha. Bora pra mais uma questão. Aqui o problema pede as cargas internas que agem em . Desa forma nós temos de pegar as forças externas (apenas a força de nesse caso) e aplica-las em . Olha só!
Passo 2
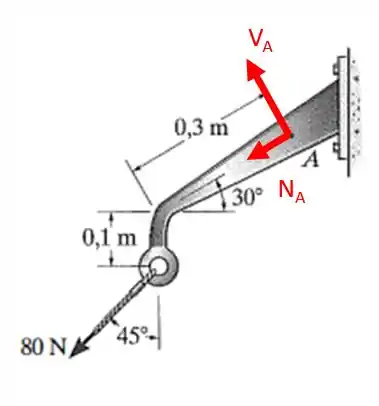
Na seção temos força cortante, normal e momento fletor. Temos que calcular todos esses esforços na seção. Vamos pegar primeiro o esforço normal, que atua na direção do eixo da barra.
Ficou assustado com aquele cosseno ali? Fica calmo. Tudo o que fizemos foi decompor a força de na direção da barra Se a força faz com a vertical e a barra está a da vertical, logo a força está a da barra.
obs: Para ficar ainda mais nítido essa questão dos ângulos se a gente imaginar que ambos estão a 45°. Nesse caso utilizaríamos o que faz total sentido, já que toda a força seria normal à barra =D
Continuando a resolução:
Passo 3
Agora, vamos calcular a força cortante (V) na barra. Que será dado por:
Note que é o mesmo caso do passo 2, mas como queremos a força perpendicular a barra, usamos seno, e não cosseno. Substituindo:
Passo 4
Agora, vamos fazer o mesmo para o momento. Ou seja:
Agora o jeito mais fácil de fazer isso é decompor a força de nas direções e e depois decompor a distância de também em e . Vamos começar pela força:
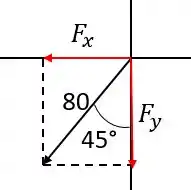
As componentes serão, portanto:
Ambas são negativas porque estão nos sentidos negativos dos respectivos eixos.
Agora para o comprimento de :
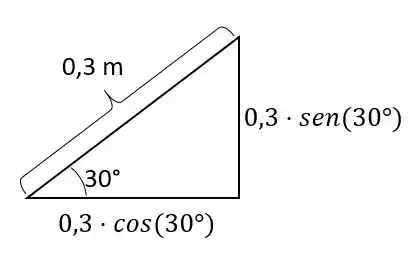
Agora nós só precisamos juntar a força horizontal com a distância vertical e a força vertical com a distância horizontal (porque para calcular o momento a força deve ser perpendicular à distância, correto?) Assim temos:
Aqui foi importanto lembrar que a distância de se soma ao termo
A mesma coisa para :
Repare que aqui nós não utilizamos o sinal de menos nos termos, então a gente tem que avaliar qual é positivo e qual é negativo pelo sentido da rotação. A força força a barra a girar no sentido horário portanto é positivo, enquanto a força força a barra a girar no sentido anti-horário portanto é negativo. Assim:
Lelmbre-se que temos de colocar o termno representando o momento interno, que é o que estamos calculando. Continuando:
Gira no sentido horário
Resposta
(sentido horário)